练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    2．已知P是边长为2的等边三角形ABC的边BC上的动点，则$\overrightarrow{AP}•（{\overrightarrow{AB}+\overrightarrow{AC}}）$的值下列判断正确的是（　　）
    A．有最大值为8B．是定值8C．有最大值为6D．是定值6

    分析 作AD⊥BC，则$\overrightarrow{AP}•（{\overrightarrow{AB}+\overrightarrow{AC}}）$=$\overrightarrow{AP}•2\overrightarrow{AD}$，根据数量积的定义式计算．

    解答 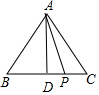解：设BC的中点为D，则AD⊥BC，
    ∴|AP|cos∠PAD=AD，$\overrightarrow{AB}+\overrightarrow{AC}$=2$\overrightarrow{AD}$，
    ∵△ABC是边长为2的等边三角形，
    ∴AD=$\sqrt{3}$，
    ∴$\overrightarrow{AP}•（{\overrightarrow{AB}+\overrightarrow{AC}}）$=$\overrightarrow{AP}•2\overrightarrow{AD}$=2×|AD|×|AP|×cos∠PAD=2×$\sqrt{3}×\sqrt{3}$=6．
    故选D．

    点评 本题考查了平面向量的数量积运算，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    12．已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的离心率为2，则其两条渐进线的夹角为（　　）
    A．$\frac{π}{6}$B．$\frac{π}{3}$C．$\frac{π}{2}$D．$\frac{2π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知集合A={y|y=$\frac{2x}{1+{x}^{2}}$}，B={x|y=ln（x+1）}，则A∩B=（　　）
    A．（-1，1）B．（-1，1]C．（-$\frac{1}{2}$，$\frac{1}{2}$）D．（-$\frac{1}{2}$，$\frac{1}{2}$]

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．有一堆规格相同的铁制（铁的密度是 7.8g/cm3）六角螺帽共重5.8kg，已知底面是正六边形，边长为12mm，内孔直径为10mm，高为10mm，问这堆螺帽大约有多少个（ π取3.14）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知函数y=$\frac{1}{3}$x3-ax2+x-5若函数在[2，+∞）上是增函数，则a的取值范围是a≤$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．设f（x）=sinx+2xf'（$\frac{π}{3}$），f'（x）是f（x）的导函数，则f'（$\frac{π}{2}$）=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．设m∈R，复数z=2m2-3m-5+（m2-2m-3）i，当m=$\frac{5}{2}$时，z为纯虚数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知定义在R上的函数f（x）满足f（-x）=-f（x），f（x+1）=f（1-x）且当x∈[0，1]时，f（x）=log2（x+1），则f（31）=-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知曲线C在平面直角坐标系xOy下的参数方程为$\left\{\begin{array}{l}x=1+\sqrt{3}cosθ\\ y=\sqrt{3}sinθ\end{array}\right.$（θ为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系．
    （1）求曲线C的普通方程及极坐标方程；
    （2）直线l的极坐标方程是$ρcos（θ-\frac{π}{6}）=3\sqrt{3}$，射线OT：$θ=\frac{π}{3}（ρ＞0）$与曲线C交于点A与直线l交于点B，求线段AB的长．

    查看答案和解析>>

    同步练习册答案