
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
分析 由1∈{x|2x2+ax-a2>0}代入得出关于参数a的不等式,解之求得a的范围,再由几何的概率模型的知识求出其概率.
解答 解:由题意1∈{x|2x2+ax-a2>0},故有2+a-a2>0,解得-1<a<2,
由几何概率模型的知识知,总的测度,区间[-3,3]的长度为6,随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}这个事件的测度为3,
故区间[-3,3]内随机地取出一个数a,使得1∈{x|2x2+ax-a2>0}的概率为$\frac{1}{2}$,
故选:D.
点评 本题考查几何概率模型,求解本题的关键是正确理解1∈{x|2x2+ax-a2>0}的意义,即得到参数a所满足的不等式,从中解出事件所对应的测度.


科目:高中数学 来源: 题型:解答题
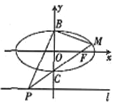 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=cos({2x+\frac{π}{2}})$ | B. | y=sin22x-cos22x | C. | y=sin2x+cos2x | D. | y=sin2xcos2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 16 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
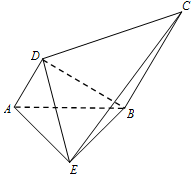 如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,
如图,AB=BE=BC=2AD=2,且AB⊥BE,∠DAB=60°,AD∥BC,BE⊥AD,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±3x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{\sqrt{3}}{3}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com