
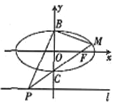
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2分析 (1)由椭圆$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1$(a>1)的长轴长是短轴长的2倍,得a=2,当直线PM过点F时,则直线PM的方程为y=$\frac{\sqrt{3}}{3}x-1$,从而得到P(-$\sqrt{3}$,-2),联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=\frac{\sqrt{3}}{3}x-1}\end{array}\right.$,得M($\frac{8\sqrt{3}}{7},\frac{1}{7}$),由此能求出$\overrightarrow{PB}•\overrightarrow{PM}$的值.
(2)设P(m,-2),且m≠0,则直线PM的方程为y=-$\frac{1}{m}x-1$,联立$\left\{\begin{array}{l}{y=-\frac{1}{m}x-1}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+$\frac{4}{{m}^{2}}$)x2+$\frac{8}{m}x$=0,解得M(-$\frac{8m}{{m}^{2}+4}$,$\frac{4-{m}^{2}}{{m}^{2}+4}$),从而得到k1=$\frac{m}{4}$,k2=-$\frac{3}{m}$,由此能求出|k1|+|k2|的最小值.
解答 解:(1)由椭圆$\frac{{x}^{2}}{{a}^{2}}+{y}^{2}=1$(a>1)的长轴长是短轴长的2倍,得a=2,
由题意B(0,1),C(0,-1),焦点F($\sqrt{3}$,0),
当直线PM过点F时,则直线PM的方程为$\frac{x}{\sqrt{3}}+\frac{y}{-1}=1$,即y=$\frac{\sqrt{3}}{3}x-1$,
令y=-2,得x=-$\sqrt{3}$,则P(-$\sqrt{3}$,-2),
联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=\frac{\sqrt{3}}{3}x-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{8\sqrt{3}}{7}}\\{y=\frac{1}{7}}\end{array}\right.$或$\left\{\begin{array}{l}{x=0}\\{y=-1}\end{array}\right.$(舍),即M($\frac{8\sqrt{3}}{7},\frac{1}{7}$),
∵$\overrightarrow{PB}$=($\sqrt{3},3$),$\overrightarrow{PM}$=($\frac{15\sqrt{3}}{7},\frac{15}{7}$),
∴$\overrightarrow{PB}•\overrightarrow{PM}$=$\frac{45}{7}+\frac{45}{7}$=$\frac{90}{7}$.
(2)设P(m,-2),且m≠0,则直线PM的斜率k=$\frac{-1-(-2)}{0-m}=-\frac{1}{m}$,
则直线PM的方程为y=-$\frac{1}{m}x-1$,
联立$\left\{\begin{array}{l}{y=-\frac{1}{m}x-1}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,化简,得(1+$\frac{4}{{m}^{2}}$)x2+$\frac{8}{m}x$=0,解得M(-$\frac{8m}{{m}^{2}+4}$,$\frac{4-{m}^{2}}{{m}^{2}+4}$),
∴k1=$\frac{\frac{4-{m}^{2}}{{m}^{2}+4}-1}{-\frac{8m}{{m}^{2}+4}}=\frac{-2{m}^{2}}{-8m}$=$\frac{m}{4}$,${k}_{2}=\frac{1-(-2)}{0-m}$=-$\frac{3}{m}$,
∴|k1|+|k2|=|-$\frac{3}{m}$|+|$\frac{m}{4}$|≥2$\sqrt{\frac{3}{4}}$=$\sqrt{3}$,
∴|k1|+|k2|的最小值为$\sqrt{3}$.
点评 本题考查向量的数量积的求法,考查两直线的斜率的绝对值的和的最小值的求法,考查椭圆、直线方程等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{8}{3}$ | C. | $\frac{6}{5}$ | D. | $\frac{12}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{5}$ | B. | $\frac{16}{5}$i | C. | $\frac{18}{5}$ | D. | $\frac{18}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{6}{13}$ | B. | $\frac{36}{5}$ | C. | $\frac{36}{13}$ | D. | $\frac{6}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com