
分析 (Ⅰ)求出导函数令f'(x)=x2-2x-3=0,解得x=-1或x=3,判断函数的单调性求出MN,然后求解直线方程.
(Ⅱ)设g(x)=f(x)$-({-\frac{8}{3}x-1})$=$\frac{1}{3}{x^3}-{x^2}-$$\frac{1}{3}x+1$,推出线段MN与曲线y=f(x)的公共点即g(x)在区间[-1,3]上的零点.令$g'(x)={x^2}-2x-\frac{1}{3}$=0,通过判断函数的极值判断函数的单调性,推出结果即可.
解答 解:(Ⅰ)令f'(x)=x2-2x-3=0,解得x=-1或x=3,
且f(x)在区间(-∞,-1),(3,+∞)上单调递增,在区间(-1,3)上单调递减,
∴x1=-1,$f({-1})=\frac{5}{3}$,x2=3,f(3)=-9,即$M({-1,\frac{5}{3}})$,N(3,-9),
∴直线MN的方程为$y+9=\frac{{\frac{5}{3}+9}}{-1-3}({x-3})$,化简得$y=-\frac{8}{3}x-1$.
(Ⅱ)设g(x)=f(x)$-({-\frac{8}{3}x-1})$=$\frac{1}{3}{x^3}-{x^2}-$$\frac{1}{3}x+1$,
则线段MN与曲线y=f(x)的公共点即g(x)在区间[-1,3]上的零点.
令$g'(x)={x^2}-2x-\frac{1}{3}$=0,解得${x_3}=1-\frac{{2\sqrt{3}}}{3}$,${x_4}=1+\frac{{2\sqrt{3}}}{3}$,
且g(x)在区间$[{-1,1-\frac{{2\sqrt{3}}}{3}})$,$({1+\frac{{2\sqrt{3}}}{3},3}]$上单调递增,
在区间$({1-\frac{{2\sqrt{3}}}{3},1+\frac{{2\sqrt{3}}}{3}})$上单调递减.
∴由$1-\frac{{2\sqrt{3}}}{3}<0<2$$<1+\frac{{2\sqrt{3}}}{3}$可得$g({1-\frac{{2\sqrt{3}}}{3}})>g(0)$=1>g(2)=-1$>g({1+\frac{{2\sqrt{3}}}{3}})$,
即$g({1-\frac{{2\sqrt{3}}}{3}})>0$,$g({1+\frac{{2\sqrt{3}}}{3}})<0$,∴g(x)在区间$({1-\frac{{2\sqrt{3}}}{3},1+\frac{{2\sqrt{3}}}{3}})$上有且仅有有一个零点.
$当-1<x≤1-\frac{2\sqrt{3}}{3}时$,有0=g(-1)<g(x),∴g(x)在$({-1,1-\frac{{2\sqrt{3}}}{3}}]$上无零点;
当$1+\frac{2\sqrt{3}}{3}≤x<3$时,有g(x)<g(3)=0,∴g(x)在$[{1+\frac{{2\sqrt{3}}}{3},3})$上无零点;
综上,g(x)在区间(-1,3)上有且仅有一个零点.
所以线段MN与曲线y=f(x)有且只有一个异于M、N的公共点.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的单调性的应用,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
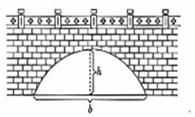
| A. | h2 | B. | 2h2 | C. | $\frac{3}{2}$h2 | D. | $\frac{7}{4}$h2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
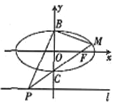 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com