
分析 (1)根据题意,分析可得4个不同的球,每个小球有4种放法,由分步计数原理计算可得答案;
(2)根据题意,恰有1个空盒,即将4个小球放入3个小盒中,且三个盒子都不空;分2步进行分析:先从4个小球中取2个放在一起,看成一个整体,再将其与另外2个小球看作三堆,并分别放入4个盒子中的3个盒子里,分别求出每一步的情况数目,由分步计数原理计算可得答案;
(3)根据题意,分2种情况讨论:①、1个盒子放3个小球,1个盒子放1个小球,②2个盒子中各放2个小球,每种情况下先分组,放进其中2个盒子中,由分步计数原理可得每种情况下的放法数目,由分类计数原理计算可得答案.
解答 解 (1)根据题意,4个不同的球,4个不同的盒子,
每个小球有4种放法,则4个小球共有4×4×4×4=44=256种放法;
(2)根据题意,恰有1个空盒,即将4个小球放入3个小盒中,且三个盒子都不空;
先从4个小球中取2个放在一起,有${C}_{4}^{2}$=6种不同的取法,
再把取出的两个小球与另外2个小球看作三堆,并分别放入4个盒子中的3个盒子里,有${A}_{4}^{3}$=24种不同的放法.
根据分步乘法计数原理,不同的放法共有6×24=144种.
(3)根据题意,恰有2个盒子不放球,也就是把4个不同的小球只放入2个盒子中,
有两类放法;第一类,1个盒子放3个小球,1个盒子放1个小球,
先把小球分成2组,有C43=4种分组方法,
再放到2个盒中有A42=12种放法,
则此时有4×12=48种放法;
第二类,2个盒子中各放2个小球,
先把小球分成2组,有$\frac{{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$=3种分组方法,
再放到2个盒中有A42=12种放法,
则此时有3×12=36种放法;
故恰有2个盒子不放球的方法共有48+36=84种.
点评 本题考查排列、组合的综合应用,注意分析题意,进行分类讨论或分步分析.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
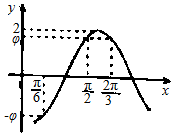 已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )
已知函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0,|φ|<π)的部分图象如图所示,则下列结论正确的是( )| A. | 函数f(x)的最小正周期为$\frac{π}{2}$ | |
| B. | 直线x=-$\frac{π}{12}$是函数f(x)图象的一条对称轴 | |
| C. | 函数f(x)在区间[-$\frac{5π}{12}$,$\frac{π}{6}$]上单调递增 | |
| D. | 将函数f(x)的图象向左平移$\frac{π}{3}$个单位,得到函数g(x)的图象,则g(x)=2sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{7}$) | B. | (-∞,3) | C. | (-∞,1)∪[2,$\sqrt{7}$) | D. | (-∞,1)∪[2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com