
分析 (1)根据题意,由二项式定理可得($\frac{1}{2}$-x)5的展开式,其中令r=3可得x3的系数,进而在($\frac{1}{2}$-x)5中,令x=1可得其各项系数之和;
(2)根据题意,由于首位数字不能为0,先分析首位数字的可能情况,再在剩下的5个数字中,任选3个,安排在百位、十位、个位,由分步计数原理计算可得答案.
解答 解:(1)根据题意,($\frac{1}{2}$-x)5中,其展开式Tr+1=C5r($\frac{1}{2}$)5-r(-x)r,
则其展开式中x3的系数为T4=C53($\frac{1}{2}$)2(-1)3=-$\frac{5}{2}$,
在($\frac{1}{2}$-x)5中,令x=1可得其各项系数之和($\frac{1}{2}$-1)5=-$\frac{1}{32}$,
(2)根据题意,分2步进行分析:
①、首位数字不能为0,则首位数字在2,3,4,5,6中选一个,则首位数字有5种情况,
②、在剩下的5个数字中,任选3个,安排在百位、十位、个位,有A53=5×4×3=60种情况,
则一共有5×60=300个满足条件的四位数.
点评 本题考查计数原理的应用以及二次项系数的性质,关键是掌握二项式定理.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | -$\frac{2}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [4,+∞) | C. | (-∞,3] | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
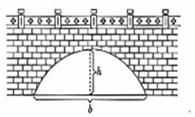
| A. | h2 | B. | 2h2 | C. | $\frac{3}{2}$h2 | D. | $\frac{7}{4}$h2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,0) | D. | (-∞,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | ①反映了建议(Ⅱ),③反映了建议(Ⅰ) | B. | ①反映了建议(Ⅰ),③反映了建议(Ⅱ) | ||
| C. | ②反映了建议(Ⅰ),④反映了建议(Ⅱ) | D. | ④反映了建议(Ⅰ),②反映了建议(Ⅱ) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com