
| A. | [3,+∞) | B. | [4,+∞) | C. | (-∞,3] | D. | (-∞,4] |
分析 f′(x)=$\frac{1}{x}$-$\frac{m(x+1)-m(x+n)}{(x+1)^{2}}$=$\frac{{x}^{2}+(mn-m+2)x+1}{x(x+1)^{2}}$.由于函数$f(x)=lnx-\frac{{m({x+n})}}{x+1}$(m>0,n∈R)在(0,+∞)上不单调,可得函数f(x)在(0,+∞)上存在极值点.因此x2+(mn-m+2)x+1=0有不相等的正的实数根.m-mn-2>0,△>0,解出即可得出.
解答 解:f′(x)=$\frac{1}{x}$-$\frac{m(x+1)-m(x+n)}{(x+1)^{2}}$=$\frac{{x}^{2}+(mn-m+2)x+1}{x(x+1)^{2}}$.
∵函数$f(x)=lnx-\frac{{m({x+n})}}{x+1}$(m>0,n∈R)在(0,+∞)上不单调,
∴函数f(x)在(0,+∞)上存在极值点.
∴x2+(mn-m+2)x+1=0有不相等的正的实数根.
∴m-mn-2>0,△=(m-2-mn)2-4>0,
由△>0化为:(m-mn-4)(1-n)>0,
∴$\left\{\begin{array}{l}{m-mn-4>0}\\{1-n>0}\end{array}\right.$,或$\left\{\begin{array}{l}{m-mn-4<0}\\{1-n<0}\end{array}\right.$,
由$\left\{\begin{array}{l}{m-mn-4>0}\\{1-n>0}\end{array}\right.$,可得:m>$\frac{4}{1-n}$>$\frac{2}{1-n}$,∴m-n>$\frac{4}{1-n}$-n=g(n),
g′(n)=$\frac{(3-n)(1+n)}{(1-n)^{2}}$,可得:n=-1时,函数g(n)取得极小值即最小值,g(-1)=3.∴λ≤3.
由$\left\{\begin{array}{l}{m-mn-4<0}\\{1-n<0}\end{array}\right.$,可得:m>$\frac{4}{1-n}$<$\frac{2}{1-n}$,舍去.
综上可得:λ≤3.
故选:C.
点评 本题考查了利用导数研究函数的单调性极值、不等式的方法,考查了推理能力与计算能力,属于难题.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
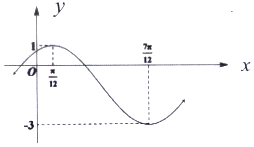 已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(wx+φ)(A>0,w>0,|φ|<\frac{π}{2})$的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\sqrt{7}$) | B. | (-∞,3) | C. | (-∞,1)∪[2,$\sqrt{7}$) | D. | (-∞,1)∪[2,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com