
分析 (1)利用已知条件推出an+1=2an,数列{an}为等比数列,公比q=2,求出通项公式.
(2)推出${b_n}={2^n}({5-n})$,方法一:通过T1<T2<T3<T4=T5>T6>推出结果.方法二利用错位相减法求和,当1≤n<4,Tn+1>Tn,当n=4,T4=T5,当n>4时,Tn+1<Tn,
综上,当且仅当k=4或5时,均有Tk≥Tn.
(3)利用裂项求和,通过对任意n∈N*均有${R_n}<\frac{2}{3}$成立,求解即可.
解答 (本小题满分13分)
解:(1)由Sn=2an-2,得Sn+1=2an+1-2两式相减,得an+1=2an+1-2an
∴an+1=2an (2分)
数列{an}为等比数列,公比q=2
又S1=2a1-2,得a1=2a1-2,a1=2∴${a_n}={2^n}$(2分)
(2)${b_{n+1}}=2{b_n}-{2^{n+1}}$$\frac{{{b_{n+1}}}}{{{2^{n+1}}}}=\frac{b_n}{2^n}-1$ (1分)
$\frac{b_n}{2^n}=\frac{b_1}{2^1}+({n-1})×({-1})$,${b_n}={2^n}({5-n})$(2分)
方法一当n≤5时,${b_n}={2^n}({5-n})$≥0(1分)
因此,T1<T2<T3<T4=T5>T6>…(1分)
∴对任意n∈N*均有T4=T5≥Tn,故k=4或5. (1分)
方法二(${T_n}=4•{2^1}+3•{2^2}+2•{2^3}+…+(5-n)•{2^n},(1)$$2{T_n}=4•{2^2}+3•{2^3}+2•{2^4}+…+(6-n)•{2^n}+(5-n)•{2^{n+1}},(2)$
两式相减,得${T_n}=-8+({2^2}+{2^3}+{2^4}+…+{2^n})+(5-n)•{2^{n+1}}$,
${T_n}=-8+\frac{{{2^2}(1-{2^{n-1}})}}{1-2}+(5-n)•{2^{n+1}}$=(6-n)•2n+1-12,(1分)${T_{n+1}}-{T_n}=(5-n)•{2^{n+2}}-(6-n)•{2^{n+1}}={2^{n+1}}(4-n)$,(1分)
当1≤n<4,Tn+1>Tn,当n=4,T4=T5,当n>4时,Tn+1<Tn,
综上,当且仅当k=4或5时,均有Tk≥Tn(1分)
(3)∵${c_n}=\frac{{{a_{\;n\;+\;1}}}}{{(1+{a_n})(1+{a_{\;n\;+\;1}})}}=\frac{{{2^{n\;+\;1}}}}{{(1+{2^n})(1+{2^{n\;+\;1}})}}=2(\frac{1}{{{2^n}+1}}-\frac{1}{{{2^{n\;+\;1}}+1}})$(1分)
∴${R_n}=2[{({\frac{1}{3}-\frac{1}{5}})+({\frac{1}{5}-\frac{1}{9}})+…({\frac{1}{{{2^n}+1}}-\frac{1}{{{2^{n+1}}+1}}})}]$=$2({\frac{1}{3}-\frac{1}{{{2^{n+1}}+1}}})$(2分)
∵对任意n∈N*均有${R_n}<\frac{2}{3}$成立,
∴$λ≥\frac{2}{3}$,
所以λ的最小值为$\frac{2}{3}$.
点评 本题考查数列的综合应用,数列通项公式的求法,数列求和,考查分析问题解决问题的能力.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [3,+∞) | B. | [4,+∞) | C. | (-∞,3] | D. | (-∞,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
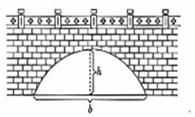
| A. | h2 | B. | 2h2 | C. | $\frac{3}{2}$h2 | D. | $\frac{7}{4}$h2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com