
| A. | $\frac{16}{5}$ | B. | $\frac{16}{5}$i | C. | $\frac{18}{5}$ | D. | $\frac{18}{5}$i |
分析 把z=3+4i代入复数z+$\frac{|z|}{z}$,然后利用复数代数形式的乘除运算化简得答案.
解答 解:∵z=3+4i,
∴$|z|=\sqrt{{3}^{2}+{4}^{2}}=5$,
∴z+$\frac{|z|}{z}$=$3+4i+\frac{5}{3+4i}=3+4i+\frac{5(3-4i)}{(3+4i)(3-4i)}$=$3+4i+\frac{3}{5}-\frac{4}{5}i=\frac{18}{5}+\frac{16}{5}i$,
∴复数z+$\frac{|z|}{z}$的虚部为$\frac{16}{5}$.
故选:A.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| 理科 | 文科 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | [0,50] | [51,100] | [101,150] | [151,200] | [201,300] | 300以上 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
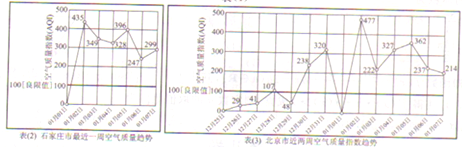
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
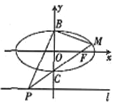 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+y2=1(a>1)的长轴长是短轴长的2倍,右焦点为F,点B,C分别是该椭圆的上、下顶点,点P是直线l:y=-2上的一个动点(与y轴交点除外),直线PC交椭圆于另一点M.记直线BM,BP的斜率分别为k1、k2查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 16 | D. | 21 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com