
���� ��1��������ɵã�2b=2�����b=1������$\frac{{x}^{2}}{{a}^{2}}$+y2=1��a��1����y=x2-$\frac{65}{16}$���ɵã�x4+$��\frac{1}{{a}^{2}}-\frac{65}{8}��$x2+$\frac{81��49}{1{6}^{2}}$=0��������ԲC��������y=x2-$\frac{65}{16}$�ĶԳ��ԣ��ɵã���=0��a��1�����a��
��2���ٵ�ֱ��l��б�ʲ�����ʱ��S��PMN=$\frac{1}{2}��2b��a$����ֱ��l��б��Ϊ0ʱ��S��PMN=$\frac{1}{2}��2b��a$��
�ڵ�ֱ��l��б�ʴ����Ҳ�Ϊ0ʱ����ֱ��l�ķ���Ϊ��y=kx������Բ�����������x2��y2��|MN|=2$\sqrt{{x}^{2}+{y}^{2}}$��������ɵã��߶�MN���д��߷���Ϊ��y=-$\frac{1}{k}$x������Բ���������ɵ�|OP|=$\sqrt{{x}^{2}+{y}^{2}}$������S��PMN=$\frac{1}{2}��$|MN|��|OP|�����������ʽ�����ʼ��ɵó���
��� �⣺��1��������ɵã�2b=2�����b=1������$\frac{{x}^{2}}{{a}^{2}}$+y2=1��a��1����y=x2-$\frac{65}{16}$���ɵã�x4+$��\frac{1}{{a}^{2}}-\frac{65}{8}��$x2+$\frac{81��49}{1{6}^{2}}$=0��
������ԲC��������y=x2-$\frac{65}{16}$�ĶԳ��ԣ��ɵã���=$��\frac{1}{{a}^{2}}-\frac{65}{8}��^{2}$-4��$\frac{81��49}{1{6}^{2}}$=0��a��1�����a=2��
����ԲC�ı�����Ϊ��$\frac{{x}^{2}}{4}$+y2=1��
��2���ٵ�ֱ��l��б�ʲ�����ʱ��S��PMN=$\frac{1}{2}��2b��a$=2��
��ֱ��l��б��Ϊ0ʱ��S��PMN=$\frac{1}{2}��2b��a$=2��
�ڵ�ֱ��l��б�ʴ����Ҳ�Ϊ0ʱ��
��ֱ��l�ķ���Ϊ��y=kx����$\left\{\begin{array}{l}{y=kx}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$�����x2=$\frac{4}{1+4{k}^{2}}$��y2=$\frac{4{k}^{2}}{1+4{k}^{2}}$��
��|MN|=2$\sqrt{{x}^{2}+{y}^{2}}$=4$\sqrt{\frac{1+{k}^{2}}{1+4{k}^{2}}}$��
������ɵã��߶�MN���д��߷���Ϊ��y=-$\frac{1}{k}$x��
����$\left\{\begin{array}{l}{y=-\frac{1}{k}x}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$���ɵ�x2=$\frac{4{k}^{2}}{{k}^{2}+4}$��y2=$\frac{4}{{k}^{2}+4}$��
��|OP|=$\sqrt{{x}^{2}+{y}^{2}}$=2$\sqrt{\frac{1+{k}^{2}}{{k}^{2}+4}}$��
S��PMN=$\frac{1}{2}��$|MN|��|OP|=$\frac{4��1+{k}^{2}��}{\sqrt{��1+4{k}^{2}����{k}^{2}+4��}}$��$\frac{4��1+{k}^{2}��}{\frac{��1+4{k}^{2}��+��{k}^{2}+4��}{2}}$=$\frac{8}{5}$�����ҽ���k=��1ʱȡ�Ⱥţ���ʱ��PMN���������СֵΪ$\frac{8}{5}$��
��$2��\frac{8}{5}$�����PMN���������СֵΪ$\frac{8}{5}$��ֱ��l�ķ���Ϊ��y=��x��
���� ���⿼������Բ�ı����̼������ʡ�һԪ���η��̵ĸ���ϵ���Ĺ�ϵ����������ʽ�����ʡ��ҳ���ʽ����������������������������������⣮


 ��ѧ�̸̳����¿α�ϵ�д�
��ѧ�̸̳����¿α�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4+6i | B�� | 4+2i | C�� | -4-2i | D�� | -2+2i�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4680 | B�� | 4770 | C�� | 5040 | D�� | 5200 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
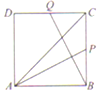
| A�� | 2 | B�� | $\frac{8}{3}$ | C�� | $\frac{6}{5}$ | D�� | $\frac{12}{25}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{16}{5}$ | B�� | $\frac{16}{5}$i | C�� | $\frac{18}{5}$ | D�� | $\frac{18}{5}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��$\frac{{e}^{2}}{2e-1}$��+�ޣ� | B�� | ��e��+�ޣ� | C�� | ��1��e�� | D�� | ��1��$\frac{{e}^{2}}{2e-1}$�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com