
| A. | 4680 | B. | 4770 | C. | 5040 | D. | 5200 |
分析 据题意,6个人中至多有1个参加”演讲团“,则分2种情况讨论:①、若有1人参加”演讲团“,②、若没有人参加”演讲团“,分别求出每一种情况下的安排方法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、若有1人参加”演讲团“,在6人中选出1人,参加”演讲团“,有C61=6种情况,
剩下的5个人参加剩下的4个社团,人数安排有1、1、1、2或1、2、2两种情况,
则有$\frac{{C}_{5}^{1}{C}_{4}^{1}{C}_{3}^{1}{C}_{2}^{2}}{{A}_{3}^{3}}$×A44+$\frac{{C}_{5}^{1}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{2}^{2}}$×A43=600种安排方法,
则此时的不同参加方法有6×600=3600种;
②、若没有人参加”演讲团“,则6人参加4个社团,人数安排有1、1、2、2或2、2、2两种情况,
此时有$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{1}{C}_{1}^{1}}{{A}_{2}^{2}{A}_{2}^{2}}$×A44+$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$×A43=1440种安排方法;
则不同参加方法有3600+1440=5040种;
故选:C.
点评 本题考查排列组合的应用,注意题目中社团人数的要求,要优先分析受到限制的元素,其次要注意正确使用分组公式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数 | [0,50] | [51,100] | [101,150] | [151,200] | [201,300] | 300以上 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
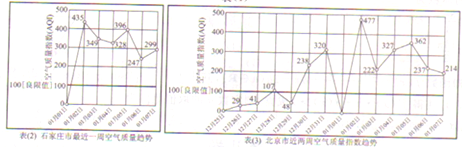
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com