
分析 利用分析法,从要证的结论入手,寻找不等式成立的充分条件,直到该条件(被找到)显然成立,从而知原结论成立.
解答 证明:要证$({m+\frac{1}{m}})•({n+\frac{1}{n}})≥\frac{25}{4}$,
只需证$mn+\frac{{{m^2}+{n^2}+1}}{mn}≥\frac{25}{4}$,
只需证$mn+\frac{2}{mn}-2≥\frac{25}{4}$,
只需证4(mn)2-33mn+8≥0,即证mn≥8或$mn≤\frac{1}{4}$,
而由$1=m+≥2\sqrt{mn}$,可得$mn≤\frac{1}{4}$显然成立,
所以不等式$({m+\frac{1}{m}})•({n+\frac{1}{n}})≥\frac{25}{4}$成立.
点评 本题考查不等式的证明,着重考查分析法证明不等式,考查推理论证能力,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | 4680 | B. | 4770 | C. | 5040 | D. | 5200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{5}$ | B. | $\frac{16}{5}$i | C. | $\frac{18}{5}$ | D. | $\frac{18}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
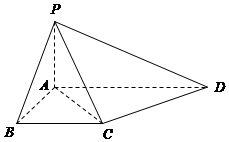 AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.
AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com