
分析 用分析法证明,结合余弦定理可得结论.
解答 证明:要证明:$\frac{1}{a-b}+\frac{1}{c-b}$=$\frac{3}{a-b+c}$,
只要证明$\frac{a+c-2b}{{({a-b})({c-b})}}$=$\frac{3}{a-b+c}$,
只要证明(a+c-2b)(a-b+c)=3(a-b)(c-b),
只要证明(a+c-b)2-b(a+c-b)=3(ac+b2-bc-ab),
只要证明b2=a2+c2-ac,
只要证明$cosB=\frac{{{a^2}+{c^2}-{b^2}}}{2ac}=\frac{1}{2}$,
只要证明B=60°,
只要证明A、B、C成等差数列,故结论成立.
点评 本题主要考查了等差关系、余弦定理的应用和解三角形问题.考查了学生综合分析问题和基本的运算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
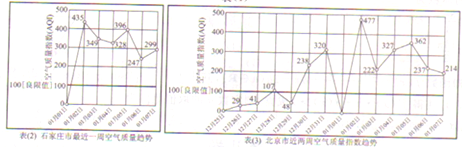
| 空气质量指数 | [0,50] | [51,100] | [101,150] | [151,200] | [201,300] | 300以上 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| y | 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| lnx | 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
| A. | $\frac{3}{5}$(e-1) | B. | $\frac{2}{5}$(e-1) | C. | $\frac{3}{5}$(e+1) | D. | $\frac{2}{5}$(e+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
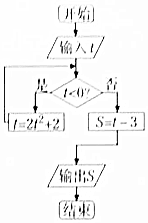
| A. | $\frac{1}{2}$ | B. | $\frac{4}{5}$ | C. | $\frac{8}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com