
分析 (I)利用抛物线上的点M到y轴的距离等于|MF2|-1,通过抛物线的定义,转化解得p=2,得到抛物线的方程,通过椭圆的右焦点F2(1,0),左焦点F1(-1,0),由|QF2|=$\frac{5}{2}$,解得Q($\frac{3}{2}$,$±\sqrt{6}$)利用椭圆的定义求出a,b.求解椭圆的方程.
(II)显然k≠0,m≠0,由$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}=4x}\end{array}\right.$消去x,推出km=1,由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1}\end{array}\right.$消去y,推出9k2-m2+8>0,求出0<m2<9,设A(x1,y1),B(x2,y2),结合韦达定理求解x0的取值范围.
解答 解:(I)∵抛物线上的点M到y轴的距离等于|MF2|-1,
∴点M到直线x=-1的距离等于点M到焦点F2的距离,----------------(1分)
得x=-1是抛物线y2=2px的准线,即-$\frac{p}{2}$=-1,解得p=2,∴抛物线的方程为y2=4x;-----------------(3分)
可知椭圆的右焦点F2(1,0),左焦点F1(-1,0),由|QF2|=$\frac{5}{2}$,得xQ+1=$\frac{5}{2}$,又yQ2=4xQ,解得Q($\frac{3}{2}$,$±\sqrt{6}$),-------(4分)
由椭圆的定义得2a=|QF1|+|QF2|=$\frac{7}{2}$+$\frac{5}{2}$=6,----------------------(5分)
∴a=3,又c=1,得b2=a2-c2=8,∴椭圆的方程为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1$.-------------------------(6分)
(II)显然k≠0,m≠0,由$\left\{\begin{array}{l}{y=kx+m}\\{{y}^{2}=4x}\end{array}\right.$消去x,得ky2-4y+4m=0,
由题意知△=16-16km=0,得km=1,--------------------------(7分)
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{9}+\frac{{y}^{2}}{8}=1}\end{array}\right.$消去y,得(9k2+8)x2+18kmx+9m2-72=0,
其中△2=(18km)2-4(9k2+8)(9m2-72)>0,
化简得9k2-m2+8>0,-----------------------------------------(9分
又k=$\frac{1}{m}$,得m4-8m2-9<0,解得0<m2<9,--------------------(10分)
设A(x1,y1),B(x2,y2),则x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{9}{9{k}^{2}+8}$<0,
由k2=$\frac{1}{{m}^{2}}$>$\frac{1}{9}$,得x0>-1,∴x0的取值范围是(-1,0).--------------(12分)
点评 本题考查椭圆以及抛物线的简单性质的应用,范围问题的处理方法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈(-∞,0),sinx0+x0<0 | B. | ?x∈(-∞,0),sinx+x≥0 | ||
| C. | ?x0∈[0,+∞),sinx0+x0<0 | D. | ?x0∈[0,+∞),sinx0+x0≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
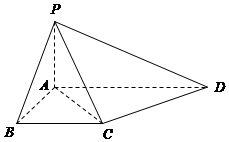 AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.
AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36种 | B. | 30种 | C. | 24种 | D. | 12种 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com