
分析 (1)根据题意,分2步进行分析:①、将6本书分成3组,每组2本,由平均分组公式可得其方法数目,②、将分好的3组对应甲、乙、丙三人,由排列数公式可得对于方法数目,由分步计数原理计算可得答案;
(2)分2步进行分析:①、将6本书分成3组,各组的本书依次为1、2、3,②、将分好的3组对应甲、乙、丙三人,由排列数公式可得对于方法数目,由分步计数原理计算可得答案;
解答 解:(1)根据题意,分2步进行分析:
①、将6本书分成3组,每组2本,有$\frac{{C}_{6}^{2}{C}_{4}^{2}{C}_{2}^{2}}{{A}_{3}^{3}}$=15种分组方法;
②、将分好的3组对应甲、乙、丙三人,有A33种情况,
则不同的分配方式有15×6=90种.
(2)根据题意,分2步进行分析:
①、将6本书分成3组,各组的本书依次为1、2、3,有C61×C52×C33种分组方法;
②、将分好的3组对应甲、乙、丙三人,有A33种情况,
则不同的分配方式有C61×C52×C33×A33=360种.
点评 本题考查排列、组合的实际应用,涉及分组问题,注意平均分租与不平均分租的公式的正确应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 66% | B. | 72.3% | C. | 67.3% | D. | 83% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
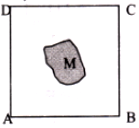 正方形ABCD的边长为2,向正方形ABCD内投掷200个点,有30个落入图形M中,则图形M的面积估计为( )
正方形ABCD的边长为2,向正方形ABCD内投掷200个点,有30个落入图形M中,则图形M的面积估计为( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com