
| 空气质量指数 | [0,50] | [51,100] | [101,150] | [151,200] | [201,300] | 300以上 |
| 空气质量状况 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
分析 (Ⅰ)求出平均数,比较即可;
(Ⅱ)求出r,根据r的范围判断即可;
(Ⅲ)设洗车店平均每天收入为X元,则X可能的取值为-200,400,700分别求出P(X=-200),P(X=400),P(X=700),求出E(X)的值即可.
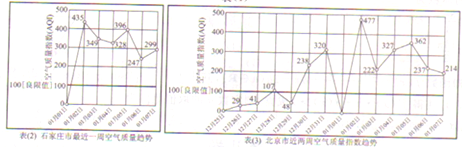
解答 解:(Ⅰ)石家庄市近一周空气污染指数的平均值为:
$\frac{0+435+349+328+396+247+299}{7}$≈293.43,
北京市近一周空气污染指数的平均数为:
$\frac{0+477+222+327+362+237+214}{7}$≈262.71,
∴石家庄市与北京市的空气都处于重度污染,
且石家庄市比北京市的污染更严重;
(Ⅱ)r=$\frac{\sum_{i=1}^{n}({x}_{i}-\overrightarrow{x})({y}_{i}-\overline{y})}{\sqrt{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}\sum_{i=1}^{n}({y}_{i}-\overline{y})}}$≈$\frac{568}{\sqrt{28×123134}}$≈$\frac{568}{1857}$≈0.31,
∵r∈[0.30,0.75),
∴石家庄市空气污染指数y与日期x之间线性相关关系一般;
(Ⅲ)设洗车店平均每天收入为X元,
则X可能的取值为-200,400,700,
P(X=-200)=$\frac{6}{14}$=$\frac{3}{7}$,
P(X=400)=$\frac{7}{14}$=$\frac{1}{2}$,
P(X=700)=$\frac{1}{14}$,
则X的分布列为:
| X | -200 | 400 | 700 |
| P | $\frac{3}{7}$ | $\frac{1}{2}$ | $\frac{1}{14}$ |
点评 本题考查了平均数问题,考查相关系数的计算以及数学期望问题,是一道中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4680 | B. | 4770 | C. | 5040 | D. | 5200 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x0∈(-∞,0),sinx0+x0<0 | B. | ?x∈(-∞,0),sinx+x≥0 | ||
| C. | ?x0∈[0,+∞),sinx0+x0<0 | D. | ?x0∈[0,+∞),sinx0+x0≥0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{16}{5}$ | B. | $\frac{16}{5}$i | C. | $\frac{18}{5}$ | D. | $\frac{18}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
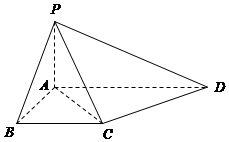 AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.
AD∥BC,∠ABC=∠PAD=90°,侧面PAD⊥底面ABCD.若 PA=AB=BC=$\frac{1}{2}$AD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com