练习册

  • 练习册
  • 试题
    相关习题
     0  247222  247230  247236  247240  247246  247248  247252  247258  247260  247266  247272  247276  247278  247282  247288  247290  247296  247300  247302  247306  247308  247312  247314  247316  247317  247318  247320  247321  247322  247324  247326  247330  247332  247336  247338  247342  247348  247350  247356  247360  247362  247366  247372  247378  247380  247386  247390  247392  247398  247402  247408  247416  266669 

    科目： 来源： 题型：选择题

    14．在下列命题中
    ①函数$y=\frac{1}{x}$的单调递减区间是（-∞，0）∪（0，+∞）．
    ②用独立性检测（2×2列联表法）来考察两个变量是否有关系时，算出的随机变量x2的值越大，说明“x与y有关系”成立的可能性越大．
    ③命题“?x∈R，x2-4x+5≤0”的否定是“?x∈R，x2-4x+5＞0”．
    ④一般地，当变量y与x之间的相关系数|r|＞0.75时，我们就认为两个变量之间具有较强的线性相关关系，若r=-0.9568，则变量y与x之间具有较强的线性关系．
    其中正确的命题个数为（　　）
    A．0B．1C．2D．3

    查看答案和解析>>

    科目： 来源： 题型：解答题

    13．某校高中三个年级共有学生1800名，各年级男生、女生的人数如表：
    高一年级高二年级高三年级
    男生290b344
    女生260ca
    已知在高中学生中随机抽取一名同学时，抽到高三年级女生的概率为0.17．
    （1）求a的值；
    （2）现用分层抽样的方法在全校抽取60名学生，则在高二年级应抽取多少名学生？
    （3）已知b≥260，c≥200，求高二年级男生比女生多的概率．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    12．已知二项式（$\sqrt{x}$-$\frac{1}{x}$）n的展开式的第6项是常数项，则n的值是（　　）
    A．5B．8C．10D．15

    查看答案和解析>>

    科目： 来源： 题型：选择题

    11．二次函数f（x）=ax2+bx+c（a＞0）的图象与x轴交点的横坐标为-5和3，则这个二次函数的单调减区间为（　　）
    A．（-∞，-1]B．[2，+∞）C．（-∞，2]D．[-1，+∞）

    查看答案和解析>>

    科目： 来源： 题型：选择题

    10．设x，y，z均大于0，则三个数：x+$\frac{1}{y}$，y+$\frac{1}{z}$，z+$\frac{1}{x}$的值（　　）
    A．都大于2B．至少有一个不大于2
    C．都小于2D．至少有一个不小于2

    查看答案和解析>>

    科目： 来源： 题型：解答题

    9．某同学参加高校自主招生3门课程的考试．假设该同学第一门课程取得优秀成绩的概率$\frac{4}{5}$，第二、第三门课程取得优秀成绩的概率分别为p，q（p＜q），且不同课程是否取得优秀成绩相互独立．记ξ为该生取得优秀成绩的课程数，其分布列为
    ξ0123
    p$\frac{6}{125}$xy$\frac{24}{125}$
    （Ⅰ）求该生至少有1门课程取得优秀成绩的概率及求p，q的值；
    （Ⅱ）求该生取得优秀成绩课程门数的数学期望Eξ．

    查看答案和解析>>

    科目： 来源： 题型：选择题

    8．当n为正整数时，定义函数N（n）表示n的最大奇因数．如N（3）=3，N（10）=5，…．记S（n）=N（1）+N（2）+N（3）+…+N（2n），则S（4）等于（　　）
    A．81B．82C．85D．86

    查看答案和解析>>

    科目： 来源： 题型：填空题

    7．函数f（x）=2sinx+x，x∈（0，2π）的单调增区间为$（0，\frac{2π}{3}）$和$（\frac{4π}{3}，2π）$．

    查看答案和解析>>

    科目： 来源： 题型：解答题

    6．已知函数f（x）=lnx+$\frac{3}{8}$x2-2x+2．
    （Ⅰ）求函数f（x）的单调区间；
    （Ⅱ）若函数f（x）在区间[e2，+∞）（k∈Z）上有零点，求k的最大值（e=2.718…）

    查看答案和解析>>

    科目： 来源： 题型：填空题

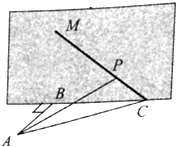    5．如图，某人在垂直于水平地面ABC的墙面前的点A处进行射击训练，已知点A到墙面的距离为AB，某目标点P沿墙面的射线CM移动，此人为了准确瞄准目标点P，需计算由点A观察点P的仰角θ的大小．若BC=10m，AC=20m，∠BCM=45°，则tanθ的最大值为$\frac{2\sqrt{3}}{3}$．（仰角θ为直线AP与平面ABC所成角）

    查看答案和解析>>

    同步练习册答案