【题目】函数的定义域为，若存在闭区间[m,n] D，使得函数满足：①在[m,n]上是单调函数；②在[m,n]上的值域为[2m,2n]，则称区间[m,n]为的“倍值区间”．下列函数中存在“倍值区间”的有 ．（填上所有正确的序号）

①；

②；

③；

④．

【题目】英州育才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分別到气象局与市医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料（表）:

该兴趣小组确定的研究方案是:先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验.

（1）求选取的组数据恰好是相邻两个月的概率；

（2）求选取的是月与月的两组数据，请根据至月份的数据，求出关于的线性回归方程；

其中回归系数公式，,.

【题目】已知是数列的前项和，且满足，等差数列的前项和为,且， .

（Ⅰ）求数列与的通项公式；

（Ⅱ）若数列的通项公式为，问是否存在互不相等的正整数， ， 使得， ， 成等差数列，且 ， ， 成等比数列？若存在，求出， ， ；若不存在，说明理由.

【题目】已知函数，下列说法正确的是（ ）

A. 该函数值域为

B. 当且仅当时，函数取最大值1

C. 该函数是以为最小正周期的周期函数

D. 当时，

【题目】海州市英才中学某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分別到气象局与某医院抄录了至月份每月号的昼夜温差情况与因患感冒而就诊的人数，得到如下资料（表）:

该兴趣小组确定的研究方案是:先从这六组数据中选取组，用剩下的组数据求线性回归方程，再用被选取的组数据进行检验.

（1）求选取的组数据恰好是相邻两个月的概率；

（2）若选取的是月与6月的两组数据，请根据至月份的数据，求出关于的线性回归方程；

（3）若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过人，则认为得到的线性回归方程是理想的，试问该小组所得线性回归方程是否理想.

其中回归系数公式，,

【题目】某学校1800名学生在一次百米测试中，成绩全部介于13秒与18秒之间，抽取其中50个样本，将测试结果按如下方式分成五组：第一组，第二组，第五组，下图是按上述分组方法得到的频率分布直方图．

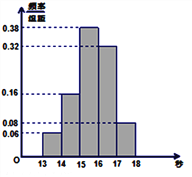
（1）若成绩小于15秒认为良好，求该样本在这次百米测试中成绩良好的人数；

（2）请估计学校1800名学生中，成绩属于第四组的人数；

（3）请根据频率分布直方图，求样本数据的众数、中位数、平均数和方差．

【题目】如图所示，在矩形中，，点是的中点，将沿折起到的位置，使二面角是直二面角.

（1）证明: ；

（2）求二面角的余弦值.

从这40名学生中按分层抽样的方式抽取10名学生在第一排发言席就座．

（1）求各大学抽取的人数；

（2）从（1）中抽取的乙大学和丁大学的学生中随机选出2名学生发言，求这2名学生来自同一所大学的概率．

【题目】为了了解某省各景点在大众中的熟知度，随机对15～65岁的人群抽样了人，回答问题“某省有哪几个著名的旅游景点？”统计结果如下图表

（1）分别求出的值；

（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，求第2，3，4组每组各抽取多少人？

（3）在（2）抽取的6人中随机抽取2人，求所抽取的人中恰好没有第3组人的概率．

①它要求被抽取样本的总体的个体数有限；

②它是从总体中逐个进行抽取的，在实践中操作起来也比较方便；

③它是一种不放回抽样；

④它是一种等可能抽样，在整个抽样过程中，每个个体被抽到的机会相等，从而保证了这种抽样方法的公平性.

A.①②③B.①②④C.①③④D.①②③④