
科目: 来源: 题型:
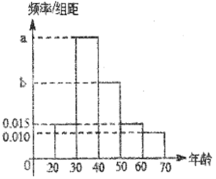
【题目】根据某电子商务平台的调查统计显示,参与调查的1000位上网购物者的年龄情况如图.
(1)已知![]() 、
、![]() ,
,![]() 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求![]() ,
,![]() 的值;
的值;
(2)该电子商务平台将年龄在![]() 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放50元的代金券,潜在消费人群每人发放80元的代金券.已经采用分层抽样的方式从参与调查的1000位上网购物者中抽取了10人,现在要在这10人中随机抽取3人进行回访,求此三人获得代金券总和![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在长方体![]() 中,
中,![]() ,
,![]() 是棱
是棱![]() 上的一点.
上的一点.
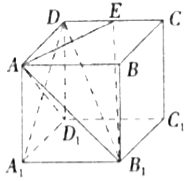
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)若![]() 是棱
是棱![]() 的中点,在棱
的中点,在棱![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出线段
?若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
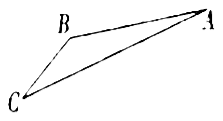
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,说明理由。

查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ).
).
(1)若![]() 的部分图像如图所示,求
的部分图像如图所示,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,求最小正实数![]() ,使得函数
,使得函数![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数是偶函数;
个单位后所对应的函数是偶函数;
(3)若![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(![]() )的池底水平铺设污水净化管道(
)的池底水平铺设污水净化管道(![]() 是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口
是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上。已知
上。已知![]() 米,
米,![]() 米,记
米,记![]() .
.
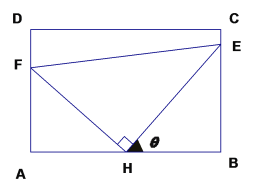
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。
查看答案和解析>>
科目: 来源: 题型:
【题目】为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元,该建筑物每年的能源消耗费用![]() (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度![]() (单位:
(单位: ![]() )满足关系
)满足关系![]() ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设![]() 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用![]() 达到最小,并求最小值。
达到最小,并求最小值。
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求函数![]() 的单调增区间;
的单调增区间;
(2)将函数![]() 的图象向左平移
的图象向左平移![]() 个单位,再向上平移1个单位,得到函数
个单位,再向上平移1个单位,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 上至少含有10个零点,求
上至少含有10个零点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com