
科目: 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() ,且
,且![]() 为常数).
为常数).
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意的![]() ,都有
,都有![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)若方程![]() 在
在![]() 上有且只有一个实根,求
上有且只有一个实根,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了了解全校学生的阅读情况,在全校采用随机抽样的方法抽取了60名学生(其中初中组和高中组各30名)进行问卷调查,并将他们在一个月内去图书馆的次数进行了统计,将每组学生去图书馆的次数分为5组: ![]() ,分别制作了如图所示的频率分布表和频率分布直方图.
,分别制作了如图所示的频率分布表和频率分布直方图.
分组 | 人数 | 频率 |
| 3 | |
| 9 | |
| 9 | |
| 0.2 | |
| 0.1 |
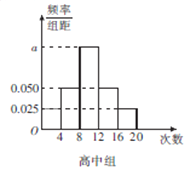
(1)完成频率分布表,并求出频率分布直方图中![]() 的值;
的值;
(2)在抽取的60名学生中,从在一个月内去图书馆的次数不少于16次的学生中随机抽取3人,并用![]() 表示抽得的高中组的人数,求
表示抽得的高中组的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知定义在区间(0,+∞)上的函数f(x)=|t(x+ ![]() )﹣5|,其中常数t>0.
)﹣5|,其中常数t>0.
(1)若函数f(x)分别在区间(0,2),(2,+∞)上单调,试求实数t的取值范围;
(2)当t=1时,方程f(x)=m有四个不相等的实根x1 , x2 , x3 , x4 . ①求四根之积x1x2x3x4的值;
②在[1,4]上是否存在实数a,b(a<b),使得f(x)在[a,b]上单调且取值范围为[ma,mb]?若存在,求出m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两种不同规格的产品,其质量按测试指标分数进行划分,其中分数不小于82分的为合格品,否则为次品.现随机抽取两种产品各100件进行检测,其结果如下:
测试指标分数 |
|
|
|
|
|
甲产品 | 8 | 12 | 40 | 32 | 8 |
乙产品 | 7 | 18 | 40 | 29 | 6 |
(1)根据以上数据,完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的有把握认为两种产品的质量有明显差异?
的有把握认为两种产品的质量有明显差异?
甲产品 | 乙产品 | 合计 | |
合格品 | |||
次品 | |||
合计 |
(2)已知生产1件甲产品,若为合格品,则可盈利40元,若为次品,则亏损5元;生产1件乙产品,若为合格品,则可盈利50元,若为次品,则亏损10元.记![]() 为生产1件甲产品和1件乙产品所得的总利润,求随机变量
为生产1件甲产品和1件乙产品所得的总利润,求随机变量![]() 的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
的分布列和数学期望(将产品的合格率作为抽检一件这种产品为合格品的概率).
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.702 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数, ![]() ),直线
),直线![]() 的极坐标方程为
的极坐标方程为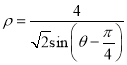 .
.
(1)写出曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)![]() 为曲线
为曲线![]() 上任意一点,
上任意一点, ![]() 为直线
为直线![]() 任意一点,求
任意一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=max{x2﹣ax+a,ax﹣a+1},其中max{x,y}= ![]() . (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
. (Ⅰ)若对任意x∈R,恒有f(x)=x2﹣ax+a,求实数a的值;
(Ⅱ)若a>1,求f(x)的最小值m(a).
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解学生的身体素质情况,现从我校学生中随机抽取10人进行体能测试,测试的分数(百分制)如茎叶图所示.根据有关国家标准,成绩不低于79分的为优秀,将频率视为概率.
(1)另从我校学生中任取3人进行测试,求至少有1人成绩是“优秀”的概率;
(2)从前文所指的这10人(成绩见茎叶图)中随机选取3人,记![]() 表示测试成绩为“优秀”的学生人数,求
表示测试成绩为“优秀”的学生人数,求![]() 的分布列及期望.
的分布列及期望.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com