
科目: 来源: 题型:
【题目】在四棱锥![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,且
,且![]() 平面
平面![]() .
.
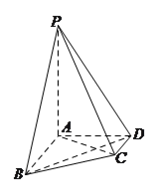
(1)设平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求证: ![]() .
.
(3)设点![]() 为线段
为线段![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知![]() ,
, ![]() ,
, ![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)记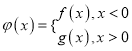 ,设
,设![]() ,
, ![]() 为函数
为函数![]() 图象上的两点,且
图象上的两点,且![]() .
.
(i)当![]() 时,若
时,若![]() 在
在![]() ,
, ![]() 处的切线相互垂直,求证:
处的切线相互垂直,求证: ![]() ;
;
(ii)若在点![]() ,
, ![]() 处的切线重合,求
处的切线重合,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在正方形![]() 中,点
中,点![]() 分别是
分别是![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 分别在线段
分别在线段![]() 上,且
上,且![]() .将
.将![]() 分别沿
分别沿![]() 折起,使点
折起,使点![]() 重合于点
重合于点![]() ,如图2所示.
,如图2所示.
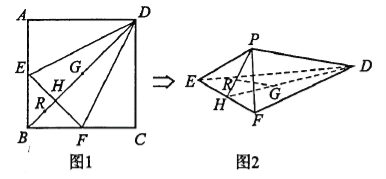
(1)求证:![]() 平面
平面![]() ;
;
(2)若正方形![]() 的边长为4,求三棱锥
的边长为4,求三棱锥![]() 的内切球的半径.
的内切球的半径.
查看答案和解析>>
科目: 来源: 题型:
【题目】完成下列进位制之间的转化.
(1)10231(4)=________(10);
(2)235(7)=________(10);
(3)137(10)=________(6);
(4)1231(5)=________(7);
(5)213(4)=________(3);
(6)1010111(2)=________(4).
查看答案和解析>>
科目: 来源: 题型:
【题目】把正整数排成如图(a)的三角形阵,然后擦去第偶数行中的所有奇数,第奇数行中的所有偶数,可得如图(b)三角形阵,现将图(b)中的正整数按从小到大的顺序构成一个数列{an},若ak=2017,则k= . 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,设双曲线![]() 的上焦点为
的上焦点为![]() ,上顶点为
,上顶点为![]() ,点
,点![]() 为双曲线虚轴的左端点,已知
为双曲线虚轴的左端点,已知![]() 的离心率为
的离心率为![]() ,且
,且![]() 的面积
的面积![]() .
.

(1)求双曲线![]() 的方程;
的方程;
(2)设抛物线![]() 的顶点在坐标原点,焦点为
的顶点在坐标原点,焦点为![]() ,动直线
,动直线![]() 与
与![]() 相切于点
相切于点![]() ,与
,与![]() 的准线相交于点
的准线相交于点![]() ,试推断以线段
,试推断以线段![]() 为直径的圆是否恒经过
为直径的圆是否恒经过![]() 轴上的某个定点
轴上的某个定点![]() ?若是,求出定点
?若是,求出定点![]() 的坐标;若不是,请说明理由.
的坐标;若不是,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
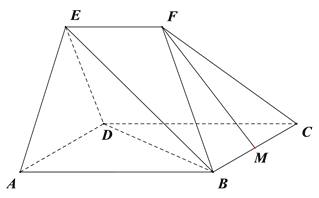
【题目】如图,在几何体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() ,
, ![]() ∥
∥![]() ,
, ![]() 为
为![]() 中点.
中点.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]()
![]() ? 若存在,求
? 若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com