
科目: 来源: 题型:
【题目】设函数fk(x)=xk+bx+c(k∈N* , b,c∈R),g(x)=logax(a>0,a≠1).
(1)若b+c=1,且fk(1)=g( ![]() ),求a的值;
),求a的值;
(2)若k=2,记函数fk(x)在[﹣1,1]上的最大值为M,最小值为m,求M﹣m≤4时的b的取值范围;
(3)判断是否存在大于1的实数a,使得对任意x1∈[a,2a],都有x2∈[a,a2]满足等式:g(x1)+g(x2)=p,且满足该等式的常数p的取值唯一?若存在,求出所有符合条件的a的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=log4(4x+1)+kx(k∈R)是偶函数.
(1)求实数k的值;
(2)设g(x)=log4(a2x+a),若f(x)=g(x)有且只有一个实数解,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
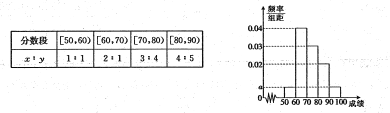
【题目】某校100名学生其中考试语文成绩的频率分布直方图所示,其中成绩分组区间是:
![]() .
.
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文某些分数段的人数![]() 与数学成绩相应分数段的人数
与数学成绩相应分数段的人数![]() 之比如下表所示,
之比如下表所示,
求数学成绩在![]() 之外的人数.
之外的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),当x>1时,有f(x)>0.
(1)求f(1),判定并证明f(x)的单调性;
(2)若f(2)=1,解不等式f(﹣x)+f(3﹣x)≥﹣2.
查看答案和解析>>
科目: 来源: 题型:
【题目】某渔业公司今年年初用98万元购进一艘渔船用于捕捞,第一年需要各种费用12万元.从第二年起包括维修费在内每年所需费用比上一年增加4万元.该船每年捕捞总收入50万元.
(1)问捕捞几年后总盈利最大,最大是多少?
(2)问捕捞几年后的平均利润最大,最大是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=kx(k≠0),且满足f(x+1)f(x)=x2+x,
(1)求函数f(x)的解析式;
(2)若函数f(x)为R上的增函数,h(x)= ![]() (f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
(f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到点
到点![]() 的距离的最大值为
的距离的最大值为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() ,
, ![]() 为抛物线
为抛物线![]() :
: ![]() 上一动点,过点
上一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某厂每日生产一种大型产品1件,每件产品的投入成本为2000元.产品质量为一等品的概率为![]() ,二等品的概率为
,二等品的概率为![]() ,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
,每件一等品的出厂价为10000元,每件二等品的出厂价为8000元.若产品质量不能达到一等品或二等品,除成本不能收回外,没生产一件产品还会带来1000元的损失.
(1)求在连续生产3天中,恰有一天生产的两件产品都为一等品的的概率;
(2)已知该厂某日生产的2件产品中有一件为一等品,求另一件也为一等品的概率;
(3)求该厂每日生产该种产品所获得的利润![]() (元)的分布列及数学期望.
(元)的分布列及数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】设f(x)是[0,1]上的不减函数,即对于0≤x1≤x2≤1有f(x1)≤f(x2),且满足(1)f(0)=0;(2)f( ![]() )=
)= ![]() f(x);(3)f(1﹣x)=1﹣f(x),则f(
f(x);(3)f(1﹣x)=1﹣f(x),则f( ![]() )=( )
)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com