
科目: 来源: 题型:
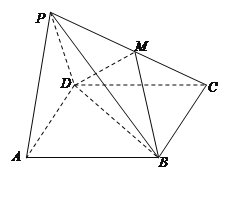
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是矩形,面
是矩形,面![]() 底面
底面![]() ,且
,且![]() 是边长为
是边长为![]() 的等边三角形,
的等边三角形, ![]() ,
, ![]() 在
在![]() 上,且
上,且![]() ∥面BDM.
∥面BDM.
(1)求直线PC与平面BDM所成角的正弦值;
(2)求平面BDM与平面PAD所成锐二面角的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)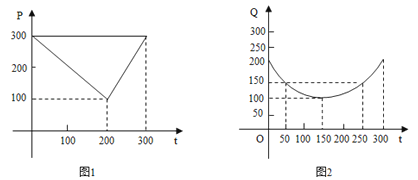
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() .
.
(1)若函数![]() 是奇函数,求实数
是奇函数,求实数![]() 的值;
的值;
(2)若对任意的实数![]() ,函数
,函数![]() (
(![]() 为实常数)的图象与函数
为实常数)的图象与函数![]() 的图象总相切于一个定点.
的图象总相切于一个定点.
① 求![]() 与
与![]() 的值;
的值;
② 对![]() 上的任意实数
上的任意实数![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1,平行四边形![]() 中,
中, ![]() ,
, ![]() ,现将
,现将![]() 沿
沿![]() 折起,得到三棱锥
折起,得到三棱锥![]() (如图2),且
(如图2),且![]() ,点
,点![]() 为侧棱
为侧棱![]() 的中点.
的中点.
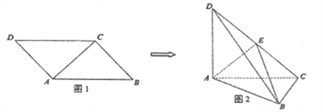
(1)求证: ![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)在![]() 的角平分线上是否存在点
的角平分线上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求
?若存在,求![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,正四棱锥P﹣ABCD中,侧棱PA与底面ABCD所成的角的正切值为![]() .
.
(1)求侧面PAD与底面ABCD所成的二面角的大小;
(2)若E是PB的中点,求异面直线PD与AE所成角的正切值;
(3)问在棱AD上是否存在一点F,使EF⊥侧面PBC,若存在,试确定点F的位置;若不存在,说明理由.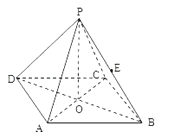
查看答案和解析>>
科目: 来源: 题型:
【题目】已知圆C:x2+y2﹣2x+4my+4m2=0,圆C1:x2+y2=25,以及直线l:3x﹣4y﹣15=0.
(1)求圆C1:x2+y2=25被直线l截得的弦长;
(2)当m为何值时,圆C与圆C1的公共弦平行于直线l;
(3)是否存在m,使得圆C被直线l所截的弦AB中点到点P(2,0)距离等于弦AB长度的一半?若存在,求圆C的方程;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
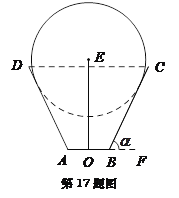
【题目】一儿童游乐场拟建造一个“蛋筒”型游乐设施,其轴截面如图中实线所示. ![]() 是等腰梯形,
是等腰梯形, ![]() 米,
米, ![]() (
(![]() 在
在![]() 的延长线上,
的延长线上, ![]() 为锐角). 圆
为锐角). 圆![]() 与
与![]() 都相切,且其半径长为
都相切,且其半径长为![]() 米.
米. ![]() 是垂直于
是垂直于![]() 的一个立柱,则当
的一个立柱,则当![]() 的值设计为多少时,立柱
的值设计为多少时,立柱![]() 最矮?
最矮?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知数列![]() ,
, ![]() 都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列
都是单调递增数列,若将这两个数列的项按由小到大的顺序排成一列(相同的项视为一项),则得到一个新数列![]() .
.
(1)设数列![]() 、
、![]() 分别为等差、等比数列,若
分别为等差、等比数列,若![]() ,
, ![]() ,
, ![]() ,求
,求![]() ;
;
(2)设![]() 的首项为1,各项为正整数,
的首项为1,各项为正整数, ![]() ,若新数列
,若新数列![]() 是等差数列,求数列
是等差数列,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() (
(![]() 是不小于2的正整数),
是不小于2的正整数),![]() ,是否存在等差数列
,是否存在等差数列![]() ,使得对任意的
,使得对任意的![]() ,在
,在![]() 与
与![]() 之间数列
之间数列![]() 的项数总是
的项数总是![]() ?若存在,请给出一个满足题意的等差数列
?若存在,请给出一个满足题意的等差数列![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com