【题目】已知集合A={x|1≤x≤5}，B={x|log2x＞1}
（1）分别求A∩B，（RB）∪A；
（2）已知集合C={x|2a﹣1≤x≤a+1}，若CA，求实数a的取值范围．

【题目】如图是某社区工会对当地企业工人月收入情况进行一次抽样调查后画出的频率分布直方图，其中第二组月收入在[1.5，2）千元的频数为300，则此次抽样的样本容量为（ ）

A.1000
B.2000
C.3000
D.4000

【题目】如图，点在以为直径的圆上，垂直与圆所在平面，为的垂心.

（1）求证：平面平面；

（2）若，求二面角的余弦值.

【题目】某班级有50名学生，其中有30名男生和20名女生，随机询问了该班五名男生和五名女生在某次数学测验中的成绩，五名男生的成绩分别为86，94，88，92，90，五名女生的成绩分别为88，93，93，88，93，下列说法正确的是（ ）
A.这种抽样方法是一种分层抽样
B.这种抽样方法是一种系统抽样
C.这五名男生成绩的方差大于这五名女生成绩的方差
D.该班男生成绩的平均数大于该班女生成绩的平均数

【题目】下列说法：
①若f（x）=ax2+（2a+b）x+2（其中x∈[﹣1，a]）是偶函数，则实数b=﹣2；
②f（x）= + 既是奇函数又是偶函数；
③若f（x+2）= ，当x∈（0，2）时，f（x）=2x ， 则f（2015）=2；
④已知f（x）是定义在R上的不恒为零的函数，且对任意的x，y∈R都满足f（xy）=xf（y）+yf（x），则f（x）是奇函数．其中所有正确命题的序号是 ．

方案一：从装有10个形状、大小完全相同的小球（其中红球3个，黑球7个）的抽奖盒中，一次性摸出3个球，其中奖规则为：若摸到3个红球，享受免单优惠；若摸出2个红球则打6折，若摸出1个红球，则打7折；若没摸出红球，则不打折.

方案二：从装有10个形状、大小完全相同的小球（其中红球3个，黑球7个）的抽奖盒中，有放回每次摸取1球，连摸3次，每摸到1次红球，立减200元.

（1）若两个顾客均分别消费了600元，且均选择抽奖方案一，试求两位顾客均享受免单优惠的概率；

（2）若某顾客消费恰好满1000元，试从概率的角度比较该顾客选择哪一种抽奖方案更合算？

【题目】已知直线的参数方程为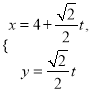（为参数），以坐标原点为极点， 轴的非负半轴为极轴建立极坐标系，圆的极坐标方程为，直线与圆交于， 两点.

（1）求圆的直角坐标方程及弦的长；

（2）动点在圆上（不与， 重合），试求的面积的最大值.

【题目】已知函数.

（1）讨论函数的单调性；

（2）当时，若函数的导函数的图象与轴交于， 两点，其横坐标分别为， ，线段的中点的横坐标为，且， 恰为函数的零点，求证： .

【题目】已知a1=3，an=2an﹣1+（t+1）2n+3m+t（t，m∈R，n≥2，n∈N*）
（1）t=0，m=0时，求证： 是等差数列；
（2）t=﹣1，m= 是等比数列；
（3）t=0，m=1时，求数列{an}的通项公式和前n项和．

【题目】设函数f（x）的定义域为D，若函数f（x）满足条件：存在[a，b]D，使f（x）在[a，b]上的值域是[2a，2b]，则称f（x）为“倍扩函数”，若函数f（x）=log2（2x+t）为“倍扩函数”，则实数t的取值范围是（ ）
A.
B.
C.
D.