
科目: 来源: 题型:
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ).
).
(Ⅰ)若 ![]()
![]() =1,求cos(
=1,求cos( ![]() ﹣x)的值;
﹣x)的值;
(Ⅱ)记f(x)= ![]()
![]() ,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
,在△ABC中,A、B、C的对边分别为a、b、c,且满足(2a﹣c)cosB=bcosC,求函数f(A)的取值范围.
查看答案和解析>>
科目: 来源: 题型:
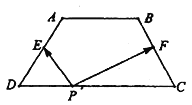
【题目】如图,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 和
和![]() 分别为
分别为![]() 与
与![]() 的中点,对于常数
的中点,对于常数![]() ,在梯形
,在梯形![]() 的四条边上恰好有8个不同的点
的四条边上恰好有8个不同的点![]() ,使得
,使得![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数![]() 的定义域为
的定义域为![]() ,如果存在正实数
,如果存在正实数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,且
,且![]() 恒成立,则称函数
恒成立,则称函数![]() 为
为![]() 上的“
上的“![]() 的型增函数”,已知
的型增函数”,已知![]() 是定义在
是定义在![]() 上的奇函数,且在
上的奇函数,且在![]() 时,
时, ![]() ,若
,若![]() 为
为![]() 上的“2017的型增函数”,则实数
上的“2017的型增函数”,则实数![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图为一简单组合体,其底面ABCD为正方形,棱PD与EC均垂直于底面ABCD,PD=2EC,N为PB的中点,求证: 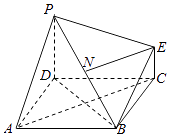
(1)平面EBC∥平面PDA;
(2)NE⊥平面PDB.
查看答案和解析>>
科目: 来源: 题型:
【题目】己知直线2x+y﹣8=0与直线x﹣2y+1=0交于点P.
(1)求过点P且平行于直线4x﹣3y﹣7=0的直线11的方程;(结果都写成一般方程形式)
(2)求过点P的所有直线中使原点O到此直线的距离最大的直线12的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() ,
, ![]() (
(![]() )
)
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)证明:当![]() 时,函数
时,函数![]() (
(![]() )有最小值.记
)有最小值.记![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值域;
的值域;
(Ⅲ)若![]() 存在两个不同的零点
存在两个不同的零点![]() ,
, ![]() (
(![]() ),求
),求![]() 的取值范围,并比较
的取值范围,并比较![]() 与0的大小.
与0的大小.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=kx+b的图象过点(2,1),且b2﹣6b+9≤0
(1)求函数f(x)的解析式;
(2)若a>0,解关于x的不等式x2﹣(a2+a+1)x+a3+3<f(x).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com