
科目: 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )(x∈R)的部分图象如图所示.
)(x∈R)的部分图象如图所示.
(Ⅰ)求函数f(x)的解析式并求函数f(x)的单调递增区间;
(Ⅱ)求函数f(x)的最小值并指出函数f(x)取最小值时相应的x的值.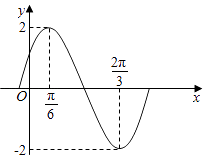
查看答案和解析>>
科目: 来源: 题型:
【题目】有下列四个说法:
①若函数f(x)=asinx+cosx(x∈R)的图象关于直线x= ![]() 对称,则a=
对称,则a= ![]() ;
;
②已知向量 ![]() =(1,2),
=(1,2), ![]() =(﹣2,m),若
=(﹣2,m),若 ![]() 与
与 ![]() 的夹角为钝角,则m<1;
的夹角为钝角,则m<1;
③当 ![]() <α<
<α< ![]() 时,函数f(x)=sinx﹣logax有三个零点;
时,函数f(x)=sinx﹣logax有三个零点;
④函数f(x)=xsinx在[﹣ ![]() ,0]上单调递减,在[0,
,0]上单调递减,在[0, ![]() ]上单调递增.
]上单调递增.
其中正确的是(填上所有正确说法的序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】一组数据的平均数是2.8,方差是3.6,若将这组数据中的每一个数据都加上60,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.57.2,3.6
B.57.2,56.4
C.62.8,63.6
D.62.8,3.6
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x+4π)=f(x)+f(2π)成立,那么函数f(x)可能是( )
A.f(x)=2sin ![]() x
x
B.f(x)=2cos2 ![]() x
x
C.f(x)=2cos2 ![]() x
x
D.f(x)=2cos ![]() x
x
查看答案和解析>>
科目: 来源: 题型:
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米圆心角为
米圆心角为![]() (弧度)的扇形景观水池,其中
(弧度)的扇形景观水池,其中![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过
的圆心,同时紧贴水池周边建一圈理想的无宽度步道,要求总预算费用不超过![]() 万元,水池造价为每平方米
万元,水池造价为每平方米![]() 元,步道造价为每米
元,步道造价为每米![]() 元.
元.
(1)当![]() 和
和![]() 分别为多少时,可使广场面积最大,并求出最大值;
分别为多少时,可使广场面积最大,并求出最大值;
(2)若要求步道长为![]() 米,则可设计出水池最大面积是多少.
米,则可设计出水池最大面积是多少.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() (
(![]() ,
, ![]() ),且对任意
),且对任意![]() ,都有
,都有![]() .
.
(Ⅰ)用含![]() 的表达式表示
的表达式表示![]() ;
;
(Ⅱ)若![]() 存在两个极值点
存在两个极值点![]() ,
, ![]() ,且
,且![]() ,求出
,求出![]() 的取值范围,并证明
的取值范围,并证明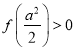 ;
;
(Ⅲ)在(Ⅱ)的条件下,判断![]() 零点的个数,并说明理由.
零点的个数,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】本着健康、低碳的生活理念,租自行车骑游的人越来越多.某自行车租车点的收费标准是每年每次租时间不超过两小时免费,超过两个小时的部分每小时收费2元(不足1小时的部分按1小时计算).现有甲、乙两人独立来该租车点租车骑游(各租一车一次).设甲、乙不超过两小时还车的概率分别为![]() ,
, ![]() ;两小时以上且不超过三小时还车的概率为
;两小时以上且不超过三小时还车的概率为![]() ,
, ![]() ;两人租车时间都不会超过四小时.
;两人租车时间都不会超过四小时.
(1)求甲、乙都在三到四小时内还车的概率和甲、乙两人所付租车费相同的概率;
(2)设甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(ωx+φ)其中ω>0,|φ|< ![]() .
.
(1)若cos ![]() cosφ﹣sin
cosφ﹣sin ![]() sinφ=0.求φ的值;
sinφ=0.求φ的值;
(2)在(1)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于 ![]() ,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象象左平移m个单位所对应的函数是偶函数.
,求函数f(x)的解析式;并求最小正实数m,使得函数f(x)的图象象左平移m个单位所对应的函数是偶函数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,侧面
的正方形,侧面![]()
底面![]() ,且
,且![]() ,
, ![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求证:面![]() 平面
平面![]() ;
;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ?说明理由.
?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com