【题目】在四棱锥P﹣ABCD中，PD⊥平面ABCD，底面是边长是1的正方形，侧棱PA与底面成45°的角，M，N，分别是AB，PC的中点；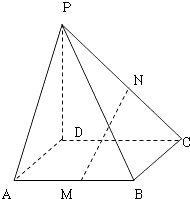

（1）求证：MN∥平面PAD；
（2）求四棱锥P﹣ABCD的体积．

【题目】设甲、乙、丙三个乒乓球协会的分别选派3，1，2名运动员参加某次比赛，甲协会运动员编号分别为A1 ， A2 ， A3 ， 乙协会编号为A4 ， 丙协会编号分别为A5 ， A6 ， 若从这6名运动员中随机抽取2名参加双打比赛．
（1）用所给编号列出所有可能抽取的结果；
（2）求丙协会至少有一名运动员参加双打比赛的概率；
（3）求参加双打比赛的两名运动员来自同一协会的概率．

【题目】如图是计算1+ + +…+ 的值的一个程序框图，其中判断框内应填的是（ ）

A.i＞10
B.i＜10
C.i＞20
D.i＜20

【题目】如图，在四边形ABCD中，AC平分∠DAB，∠ABC=60°，AC=6，AD=5，S△ADC= ，求AB的长．

【题目】已知两个无穷数列和的前项和分别为， ， ， ，对任意的，都有．

（1）求数列的通项公式；

（2）若 为等差数列，对任意的，都有．证明： ；

（3）若 为等比数列， ， ，求满足 的值．

【题目】某景区修建一栋复古建筑，其窗户设计如图所示．圆的圆心与矩形对角线的交点重合，且圆与矩形上下两边相切(为上切点)，与左右两边相交(， 为其中两个交点)，图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m，且．设，透光区域的面积为．

（1）求关于的函数关系式，并求出定义域；

（2）根据设计要求，透光区域与矩形窗面的面积比值越大越好．当该比值最大时，求边的长度．

【题目】已知函数， ．

（1）当时，求函数的单调增区间；

（2）设函数， ．若函数的最小值是，求的值；

（3）若函数， 的定义域都是，对于函数的图象上的任意一点，在函数的图象上都存在一点，使得，其中是自然对数的底数， 为坐标原点．求的取值范围．

【题目】设等差数列{an}的前n项和为Sn ， 已知a3=24，S11=0．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）求数列{an}的前n项和Sn；
（Ⅲ）当n为何值时，Sn最大，并求Sn的最大值．

【题目】某市有大型超市200家、中型超市400家、小型超市1400 家．为掌握各类超市的营业情况，现按分层抽样方法抽取一个容量为100的样本，应抽取中型超市（ ）
A.70家
B.50家
C.20家
D.10家