
科目: 来源: 题型:
【题目】已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,在以极点为直角坐标原点
,在以极点为直角坐标原点![]() ,极轴为
,极轴为![]() 轴的正半轴建立的平面直角坐标系
轴的正半轴建立的平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为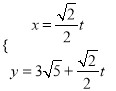 (
(![]() 为参数).
为参数).
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)在平面直角坐标系中,设曲线![]() 经过伸缩变换
经过伸缩变换![]() :
: 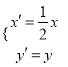 得到曲线
得到曲线![]() ,若
,若![]() 为曲线
为曲线![]() 上任意一点,求点
上任意一点,求点![]() 到直线
到直线![]() 的最小距离.
的最小距离.
查看答案和解析>>
科目: 来源: 题型:
【题目】几个月前,成都街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.
为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展 共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系;
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() ,
,![]() 的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为
的被调查人中各随机选取两人进行调查,记选中的4人中支持发展共享单车的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x3﹣ ![]() ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
ax2 , 且关于x的方程f(x)+a=0有三个不等的实数根,则实数a的取值范围是( )
A.(﹣∞,﹣ ![]() )∪(0,
)∪(0, ![]() )
)
B.(﹣ ![]() ,0)∪(
,0)∪( ![]() ,+∞)
,+∞)
C.(﹣ ![]() ,
, ![]() )
)
D.(﹣∞,﹣ ![]() )∪(
)∪( ![]() ,+∞)
,+∞)
查看答案和解析>>
科目: 来源: 题型:
【题目】对两个变量y和x进行回归分析,得到一组样本数据:(x1 , y1),(x2 , y2),…,(xn , yn),则下列说法中不正确的是( )
A.由样本数据得到的回归方程 ![]() =
= ![]() x+
x+ ![]() 必过样本中心(
必过样本中心( ![]() ,
, ![]() )
)
B.残差平方和越小的模型,拟合的效果越好
C.用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好
D.两个随机变量的线性相关性越强,相关系数的绝对值越接近于1
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=sin(ωx+)(ω>0)的部分图象如图所示,下面结论正确的个数是( )
①函数f(x)的最小正周期是2π
②函数f(x)的图象可由函数g(x)=sin2x的图象向左平移 ![]() 个单位长度得到
个单位长度得到
③函数f(x)的图象关于直线x= ![]() 对称
对称
④函数f(x)在区间[ ![]() ]上是增函数.
]上是增函数.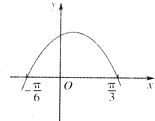
A.3
B.2
C.1
D.0
查看答案和解析>>
科目: 来源: 题型:
【题目】下列叙述正确的个数是( )
①若a>b,则ac2>bc2;
②若命题p为真命题题,命题q为假命题,则p∨q为假命题;
③若命题p:x0∈R,x ![]() ﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
﹣x0+1≤0,则¬p:x∈R,x2﹣x+1>0.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=ex(ax+b)(其中e=2.71828…),g(x)=x2+2bx+2,已知它们在x=0处有相同的切线.
(1)求函数f(x),g(x)的解析式;
(2)若函数F(x)=f(x)+g(x)﹣2(ex+x),试判断函数F(x)的零点个数,并说明理由;
(3)若函数f(x)在[t,t+1](t>﹣3)上的最小值为φ(t),解关于t的不等式φ(t)≤4e2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com