【题目】在定义域内给定区间[a，b]上存在x0（a＜x0＜b）满足f（x0）= ，则称函数y=f（x）在区间[a，b]上的“平均值函数”，x0是它的一个均值点．若函数f（x）=﹣x2+mx+1是[﹣1，1]上的平均值函数，则实数m的取值范围是

【题目】集合I={1，2，3，4，5}，集合A，B为集合I的两个非空子集，若集合A中元素的最大值小于集合B中元素的最小值，则满足条件的A，B的不同情形有（ ）种．
A.46
B.47
C.48
D.49

【题目】设f（x）是奇函数，且在（0，+∞）内是增函数，又f（﹣3）=0，则（x﹣1）f（x）＜0的解集是（ ）
A.{x|﹣3＜x＜0或1＜x＜3}
B.{x|1＜x＜3}
C.{x|x＞3或x＜﹣3}
D.{x|x＜﹣3或x＞1}

在极坐标系中，圆的极坐标方程为.若以极点为原点，极轴所在直线为轴建立平面直角坐标系.

（Ⅰ）求圆的参数方程；

（Ⅱ）在直角坐标系中，点是圆上动点，试求的最大值，并求出此时点的直角坐标.

【题目】已知函数， .

（Ⅰ）证明： ，直线都不是曲线的切线；

（Ⅱ）若，使成立，求实数的取值范围.

【题目】函数f（x）= ，（x∈（﹣∞，0]∪[2，+∞））的值域为（ ）
A.[0，4]
B.[0，2）∪（2，4]
C.（﹣∞，0]∪[4，+∞）
D.（﹣∞，2）∪（2，+∞）

【题目】已知椭圆： （）的离心率为， 、分别是它的左、右焦点，且存在直线，使、关于的对称点恰好是圆： （， ）的一条直径的两个端点.

（Ⅰ）求椭圆的方程；

（Ⅱ）设直线与抛物线（）相交于、两点，射线、与椭圆分别相交于点、.试探究：是否存在数集，当且仅当时，总存在，使点在以线段为直径的圆内？若存在，求出数集；若不存在，请说明理由.

【题目】函数f（x）=x2﹣mx（m＞0）在区间[0，2]上的最小值记为g（m）
（1）若0＜m≤4，求函数g（m）的解析式；
（2）定义在（﹣∞，0）∪（0，+∞）的函数h（x）为偶函数，且当x＞0时，h（x）=g（x），若h（t）＞h（4），求实数t的取值范围．

【题目】在平面直角坐标系中， 分别为椭圆： 的左、右焦点, 为短轴的一个端点， 是椭圆上的一点，满足，且的周长为.

（1）求椭圆的方程；

（2）设点是线段上的一点，过点且与轴不垂直的直线交椭圆于两点，若是以为顶点的等腰三角形，求点到直线距离的取值范围.

【题目】某试验田分别种植了甲乙两种水稻，为了研究这两种水稻的产量，抽检了甲、乙两种水稻的谷穗各1000株．经统计，得到每株谷穗的粒数的频率分布直方图如图：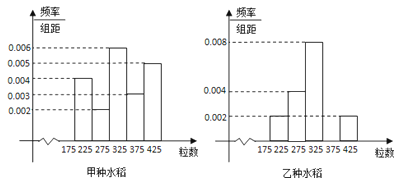

（Ⅰ）求乙种水稻谷穗的粒数落在[325，375）之间的频率，并将频率分布直方图补齐；
（Ⅱ）试根据频率分布直方图估计甲种水稻谷穗粒数的中位数与平均数（精确到0.1）；
（Ⅲ）根据频率分布直方图，请至少从两方面对甲乙两种水稻谷穗的粒数作出评价．