
科目: 来源: 题型:
【题目】某研究小组为了研究某品牌智能手机在正常使用情况下的电池供电时间,分别从该品牌手机的甲、乙两种型号中各选取![]() 部进行测试,其结果如下:
部进行测试,其结果如下:
甲种手机供电时间(小时) |
|
|
|
|
|
|
乙种手机供电时间(小时) |
|
|
|
|
|
|
(1)求甲、乙两种手机供电时间的平均值与方差,并判断哪种手机电池质量好;
(2)为了进一步研究乙种手机的电池性能,从上述![]() 部乙种手机中随机抽取
部乙种手机中随机抽取![]() 部,记所抽
部,记所抽![]() 部手机供电时间不小于
部手机供电时间不小于![]() 小时的个数为
小时的个数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
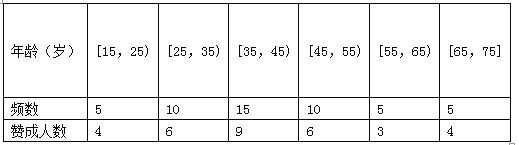
【题目】私家车的尾气排放是造成雾霾天气的重要因素之一,因此在生活中我们应该提倡低碳生活,少开私家车,尽量选择绿色出行方式,为预防雾霾出一份力.为此,很多城市实施了机动车车尾号限行,我市某报社为了解市区公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
(Ⅰ)完成被调查人员的频率分布直方图;
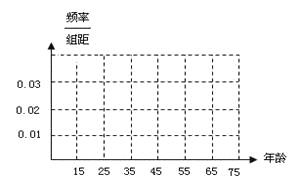
(Ⅱ)若从年龄在[15,25),[25,35)的被调查者中各随机选取2人进行追踪调查,求恰有2人不赞成的概率;
(Ⅲ)在(Ⅱ)的条件下,再记选中的4人中不赞成“车辆限行”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系中,以原点为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C:sinθ=ρcos2θ,过点M(﹣1,2)的直线l:  (t为参数)与曲线C相交于A、B两点.求:
(t为参数)与曲线C相交于A、B两点.求:
(1)线段AB的长度;
(2)点M(﹣1,2)到A、B两点的距离之积.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB,⊙O交直线OB于E、D,连接EC、CD. 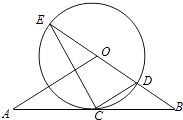
(1)求证:直线AB是⊙O的切线;
(2)若tan∠CED= ![]() ,⊙O的半径为3,求OA的长.
,⊙O的半径为3,求OA的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求曲线
,求曲线![]() 在点
在点![]() 处的切线;
处的切线;
(2)若函数![]() 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某险种的基本保费为![]() (单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:
(单位:元),继续购买该险峰种的投保人称为续保人,续保人的本年度的保费与其上处度的出险次数的关联如下:

设该险种一续保人一年内出险次数与相应概率如下:

(1) 求一续保人本年度的保费高于基本保费的概率;
(2) 若一续保人本年度的保费高于基本保费用,求其保费比基本保费高出60%的概率;
(3) 求续保人本年度的平均保费与基本保费的比值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l:(2 ![]() +1)x+(
+1)x+( ![]() +2)y+2
+2)y+2 ![]() +2=0(
+2=0( ![]() ∈R),有下列四个结论:
∈R),有下列四个结论:
直线l经过定点(0,-2);
②若直线l在x轴和y轴上的截距相等,则 ![]() =1;
=1;
当 ![]() ∈[1, 4+3
∈[1, 4+3 ![]() ]时,直线l的倾斜角q∈[120°,135°];
]时,直线l的倾斜角q∈[120°,135°];
④当 ![]() ∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为
∈(0,+∞)时,直线l与两坐标轴围成的三角形面积的最小值为 ![]() .
.
其中正确结论的是(填上你认为正确的所有序号).
查看答案和解析>>
科目: 来源: 题型:
【题目】设A,B是x轴上的两点,点P的横坐标为2,且|PA|=|PB|,若直线PA的方程为x-y+1=0,则直线PB的方程是( ).
A.x+y-5=0
B.2x-y-1=0
C.2y-x-4=0
D.2x+y-7=0
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C的左右顶点分别为A(﹣2,0),B(2,0),椭圆上除A、B外的任一点C满足kACkBC=﹣ ![]() .
. 
(1)求椭圆C的标准方程;
(2)过点P(4,0)任作一条直线l与椭圆C交于不同的两点M,N,在x轴上是否存在点Q,使得∠PQM+∠PQN=180°?若存在,求出点Q的坐标;若不存在,请说明现由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com