
科目: 来源: 题型:
【题目】如果函数f(x)是定义在(﹣3,3)上的奇函数,当0<x<3时,函数f(x)的图象如图所示,那么不等式f(x)cosx<0的解集是( ) 
A.(﹣3,﹣ ![]() )∪(0,1)∪(
)∪(0,1)∪( ![]() ,3)
,3)
B.(﹣ ![]() ,﹣1)∪(0,1)∪(
,﹣1)∪(0,1)∪( ![]() ,3)
,3)
C.(﹣3,﹣1)∪(0,1)∪(1,3)
D.(﹣3,﹣ ![]() )∪(0,1)∪(1,3)
)∪(0,1)∪(1,3)
查看答案和解析>>
科目: 来源: 题型:
【题目】“微信运动”已成为当下热门的健身方式,小王的微信朋友圈内也有大量好友参与了“微信运动”,他随机选取了其中的40人(男、女各20人),记录了他们某一天的走路步数,并将数据整理如下:
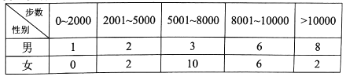
(1)若采用样本估计总体的方式,试估计小王的所有微信好友中每日走路步数超过5000步的概率;
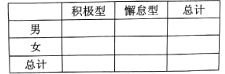
(2)已知某人一天的走路步数超过8000步被系统评定“积极型”,否则为“懈怠型”,根据题意完成下面的![]() 列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
列联表,并据此判断能否有95%以上的把握认为“评定类型”与“性别”有关?
附: 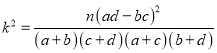 ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目: 来源: 题型:
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每台新机随机购买第一盒墨150元,优惠0元;再每多买一盒墨都要在原优惠基础上多优惠一元,即第一盒墨没有优惠,第二盒墨优惠一元,第三盒墨优惠2元,……,依此类推,每台新机最多可随新机购买25盒墨.平时购买墨盒按零售每盒200元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如下表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
以这十台打印机消耗墨盒数的频率代替一台打印机消耗墨盒数发生的概率,记ξ表示两台打印机5年消耗的墨盒数.
(1)求ξ的分布列;
(2)若在购买两台新机时,每台机随机购买23盒墨,求这两台打印机正常使用五年在消耗墨盒上所需费用的期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】超市某种绿色食品,过去20个月该食品的月市场需求量![]() (单位:
(单位: ![]() ,
, ![]() )即每月销售的数据记录如下:
)即每月销售的数据记录如下:
137 108 114 121 115 135 122 140 128 139
125 140 130 125 105 115 133 124 149 115
对这20个数据按组距10进行分组,并统计整理,绘制了如下尚不完整的统计图表:

(Ⅰ)写出![]() ,
, ![]() 的值.若视
的值.若视![]() 分布在各区间内的频率为相应的概率,试计算
分布在各区间内的频率为相应的概率,试计算![]() ;
;
(Ⅱ)记![]() 组月市场需求量数据的平均数与方差分别为
组月市场需求量数据的平均数与方差分别为![]() ,
, ![]() ,
, ![]() 组月市场需求量数据的平均数与方差分别为
组月市场需求量数据的平均数与方差分别为![]() ,
, ![]() ,试分别比较
,试分别比较![]() 与
与![]() ,
, ![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)为保证该绿色产品的质量,超市规定该产品仅在每月一日上架销售,每月最后一日对所有未售出的产品进行下架处理.若超市每售出![]() 该绿色食品可获利润5元,未售出的食品每
该绿色食品可获利润5元,未售出的食品每![]() 亏损3元,并且超市为下一个月采购了
亏损3元,并且超市为下一个月采购了![]() 该绿色食品,求超市下一个月销售该绿色食品的利润
该绿色食品,求超市下一个月销售该绿色食品的利润![]() 的分布列及数学期望
的分布列及数学期望![]() .(以分组的区间中点值代表该组的各个值,并以月市场需求量落入该区间的频率作为月市场需求量取该组区间中点值的概率)
.(以分组的区间中点值代表该组的各个值,并以月市场需求量落入该区间的频率作为月市场需求量取该组区间中点值的概率)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)=logmx(m为常数,m>0且m≠1),设f(a1),f(a2),…,f(an)(n∈N+)是首项为4,公差为2的等差数列.
(Ⅰ)求证:数列logman=2n+2,{an}是等比数列;
(Ⅱ)若bn=anf(an),记数列{bn}的前n项和为Sn , 当m= ![]() 时,求Sn .
时,求Sn .
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值,并用an﹣1表示an;
(2)求数列{an}的通项公式;
(3)设Tn= ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() ,求证:Tn<
,求证:Tn< ![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】在矩形![]() 中,
中, ![]() ,
, ![]() 是边
是边![]() 的中点,如图(1),将
的中点,如图(1),将![]() 沿直线
沿直线![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图(2).
,如图(2).
(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知![]() ,
, ![]() ,
, ![]() 分别是线段
分别是线段![]() ,
, ![]() ,
, ![]() 上的点,且
上的点,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.


查看答案和解析>>
科目: 来源: 题型:
【题目】已知曲线![]() 上的点到二定点
上的点到二定点![]() 、
、![]()
![]() 的距离之和为定值
的距离之和为定值![]() ,以
,以![]() 为圆心半径为4的圆
为圆心半径为4的圆![]() 与
与![]() 有两交点,其中一交点为
有两交点,其中一交点为![]() ,
, ![]() 在y轴正半轴上,圆
在y轴正半轴上,圆![]() 与x轴从左至右交于
与x轴从左至右交于![]() 二点,
二点, ![]() .
.
(1)求曲线![]() 、
、![]() 的方程;
的方程;
(2)曲线![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() ,过
,过![]() 点的直线
点的直线![]() 与曲线
与曲线![]() 交于
交于![]() 二点,过
二点,过![]() 做
做![]() 的切线
的切线![]() ,
, ![]() 交于
交于![]() .当
.当![]() 在x轴上方时,是否存在点
在x轴上方时,是否存在点![]() ,满足
,满足![]() ,并说明理由.
,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com