
科目: 来源: 题型:
【题目】已知集合A={x|x=a0+a1×2+a2×22+a3×23},其中ai∈{0,1,2}(i=0,1,2,3),且a0≠0,则A中所有元素之和等于 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示的分数三角形,称为“莱布尼茨三角形”.这个三角形的规律是:各行中的每一个数,都等于后面一行中与它相邻的两个数之和(例如第4行第2个数 ![]() 等于第5行中的第2个数
等于第5行中的第2个数 ![]() 与第3个数
与第3个数 ![]() 之和).则
之和).则
在“莱布尼茨三角形”中,第10行从左到右第2个数到第8个数中各数的倒数之和为( )
A.5010
B.5020
C.10120
D.10130
查看答案和解析>>
科目: 来源: 题型:
【题目】2016年某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计60吨厨余垃圾,假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱和“其他垃圾”箱的投放量分别为x,y,z,其中x>0,x+y+z=60,则数据x,y,z的标准差的最大值为 . (注:方差 ![]() ,其中
,其中 ![]() 为x1 , x2 , …,xn的平均数)
为x1 , x2 , …,xn的平均数)
查看答案和解析>>
科目: 来源: 题型:
【题目】(本小题满分10分)选修4—5:不等式选讲
设函数f(x)=|2x﹣7|+1.
(Ⅰ)求不等式f(x)≤x的解集;
(Ⅱ)若存在x使不等式f(x)﹣2|x﹣1|≤a成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学为了了解全校学生的上网情况,在全校采取随机抽样的方法抽取了![]() 名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为
名学生(其中男女生人数恰好各占一半)进行问卷调查,并进行了统计,按男女分为两组,再将每组学生的月上网次数分为![]() 组:
组: ![]() ,得到如图所示的频率分布直方图:
,得到如图所示的频率分布直方图:
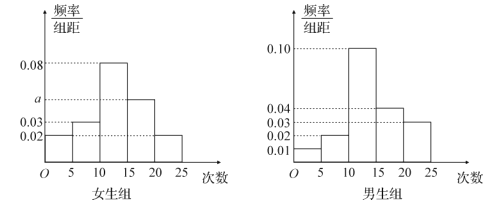
(1)写出![]() 的值;
的值;
(2)求抽取的![]() 名学生中月上网次数不少于
名学生中月上网次数不少于![]() 次的学生的人数;
次的学生的人数;
(3)在抽取的![]() 名学生中,从月上网次数少于
名学生中,从月上网次数少于![]() 次的学生中随机抽取
次的学生中随机抽取![]() 人,求至少抽取到
人,求至少抽取到![]() 名男生的概率.
名男生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某同学从区间[﹣1,1]随机抽取2n个数x1 , x2 , …,xn , y1 , y2 , …,yn , 构成n个数对(x1 , y1),(x2 , y2),…(xn , yn),该同学用随机模拟的方法估计n个数对中两数的平方和小于1(即落在以原点为圆心,1为半径的圆内)的个数,则满足上述条件的数对约有个.
查看答案和解析>>
科目: 来源: 题型:
【题目】假设要抽查某企业生产的某种品牌的袋装牛奶的质量是否达标,现从700袋牛奶中抽取50袋进行检验.利用随机数表抽取样本时,先将700袋牛奶按001,002,…,700进行编号,如果从随机数表第3行第1组数开始向右读,最先读到的5袋牛奶的编号是614,593,379,242,203,请你以此方式继续向右读数,随后读出的3袋牛奶的编号是 . (下列摘取了随机数表第1行至第5行) 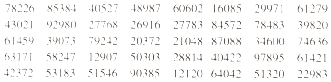
查看答案和解析>>
科目: 来源: 题型:
【题目】给出下列四个命题:
①由样本数据得到的回归方程 ![]() 必过样本点的中心(
必过样本点的中心( ![]() ,
, ![]() );
);
②用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好;
③若线性回归方程为 ![]() =3﹣2.5x,则变量x每增加1个单位时,y平均减少2.5个单位;
=3﹣2.5x,则变量x每增加1个单位时,y平均减少2.5个单位;
④在残差图中,残差点分布的带状区域的宽度越窄,残差平方和越小.
上述四个命题中,正确命题的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】已知直线l: 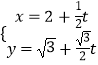 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2.
(1)若点M的直角坐标为(2, ![]() ),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
),直线l与曲线C交于A、B两点,求|MA|+|MB|的值;
(2)设曲线C经过伸缩变换 ![]() 得到曲线C′,求曲线C′的内接矩形周长的最大值.
得到曲线C′,求曲线C′的内接矩形周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com