
科目: 来源: 题型:
【题目】随着人们对环境关注度的提高,绿色低碳出行越来越受到市民重视. 为此贵阳市建立了公共自行车服务系统,市民凭本人二代身份证到自行车服务中心办理诚信借车卡借车,初次办卡时卡内预先赠送20积分,当积分为0时,借车卡将自动锁定,限制借车,用户应持卡到公共自行车服务中心以1元购1个积分的形式再次激活该卡,为了鼓励市民租用公共自行车出行,同时督促市民尽快还车,方便更多的市民使用,公共自行车按每车每次的租用时间进行扣分收费,具体扣分标准如下:
①租用时间不超过1小时,免费;
②租用时间为1小时以上且不超过2小时,扣1分;
③租用时间为2小时以上且不超过3小时,扣2分;
④租用时间超过3小时,按每小时扣2分收费(不足1小时的部分按1小时计算).
甲、乙两人独立出行,各租用公共自行车一次,两人租车时间都不会超过3小时,设甲、乙租用时间不超过1小时的概率分别是0.4和0.5;租用时间为1小时以上且不超过2小时的概率分别是0.4和0.3.
(1)求甲、乙两人所扣积分相同的概率;
(2)设甲、乙两人所扣积分之和为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某军工企业生产一种精密电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:R(x)= 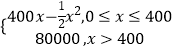 其中x是仪器的月产量.
其中x是仪器的月产量.
(1)将利润表示为月产量的函数;
(2)当月产量为何值时,公司所获利润最大?最大利润是多少元?(总收益=总成本+利润.)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,A,B,C,D为空间四点.在△ABC中,AB=2,AC=BC= ![]() .等边三角形ADB以AB为轴运动.
.等边三角形ADB以AB为轴运动. 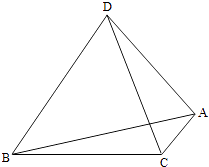
(1)当平面ADB⊥平面ABC时,求CD;
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
查看答案和解析>>
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,其中
,其中![]() 为参数,
为参数, ![]() ,再以坐标原点
,再以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,其中
,其中![]() ,
, ![]() ,直线
,直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 的值;
的值;
(2)已知点![]() ,且
,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四棱锥P﹣ABCD底面是正方形,PA⊥底面ABCD,E,F分别为PA,PD中点. 
(1)求证:EF∥面PBC
(2)求证:平面PBC⊥平面PAB.
查看答案和解析>>
科目: 来源: 题型:
【题目】将一个半径适当的小球放入如图所示的容器自上方的入口处,小球自由下落,小气在下落的过程中,将遇到黑色障碍物3次,最后落入A袋或B袋中,已知小球每次遇到障碍物时,向左、右两边下落的概率分别是 ![]() ,
, ![]()
(1)分别求出小球落入A袋和B袋中的概率;
(2)在容器 入口处依次放入4个小球,记ξ为落入B袋中的小球个数,求ξ的分布列和数学期望.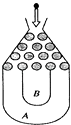
查看答案和解析>>
科目: 来源: 题型:
【题目】小丽今天晚自习准备复习历史、地理或政治中的一科,她用数学游戏的结果来决定选哪一科,游戏规则是:在平面直角坐标系中,以原点![]() 为起点,再分别以
为起点,再分别以![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积
这5个点为终点,得到5个向量,任取其中两个向量,计算这两个向量的数量积![]() ,若
,若![]() ,就复习历史,若
,就复习历史,若![]() ,就复习地理,若
,就复习地理,若![]() ,就复习政治.
,就复习政治.
(1)写出![]() 的所有可能取值;
的所有可能取值;
(2)求小丽复习历史的概率和复习地理的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点A(1,3)B(3,1),C(﹣1,0)求:
(1)求BC及BC边上的中线所在直线的方程;
(2)求BC边上的垂直平分线所在直线方程;
(3)求△ABC的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,计算得 ![]() =80,
=80, ![]() =20,
=20, ![]() i=184,
i=184, ![]() =720.
=720.
(1)求家庭的月储蓄对月收入的回归方程;
(2)判断月收入与月储蓄之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com