①函数的一个对称中心为；

②在中， 是的中点，则；

③在中， 是的充要条件；

④定义，已知，则的最大值为.

【题目】给出下列三个类比结论．
①（ab）n=anbn与（a+b）n类比，则有（a+b）n=an+bn；
②loga（xy）=logax+logay与sin（α+β）类比，则有sin（α+β）=sinαsinβ；
③（a+b）2=a2+2ab+b2与（ + ）2类比，则有（ + ）2= 2+2 + 2；
其中结论正确的个数是（ ）
A.0
B.1
C.2
D.3

【题目】用数学归纳法证明1+2+3+…+n2= ，则当n=k+1时左端应在n=k的基础上加上（ ）
A.k2+1
B.（k+1）2
C.
D.（k2+1）+（k2+2）+（k2+3）+…+（k+1）2

【题目】已知圆心在轴上的圆与直线切于点.

（1）求圆的标准方程；

（2）已知，经过原点，且斜率为正数的直线与圆交于两点.

（ⅰ）求证： 为定值；

（ⅱ）求的最大值.

【题目】三棱柱，侧棱与底面垂直， , 分别是的中点．

（1）求证： 平面；

（2）求证：平面平面．

（1）若本次抽取的样本数据有30 天是在供暖季，其中有8 天为严重污染．根据提
供的统计数据，完成下面的2×2 列联表，并判断是否有95%的把握认为“该城市本年的
空气严重污染与供暖有关”？

（2）已知某企业每天的经济损失y（单位：元）与空气质量指数x 的关系式为y= 试估计该企业一个月（按30 天计算）的经济损失的数学期望．
参考公式：K2=

【题目】设a，b为两条直线，α，β为两个平面，下列四个命题中，正确的命题是（ ）
A.若a，b与α所成的角相等，则α∥b
B.若a∥α，b∥β，α∥β，则a∥b
C.若aα，bβ，α∥b，则α∥β
D.若a⊥α，b⊥β，α⊥β，是a⊥b

【题目】已知函数f（x）=|x|+ ﹣1（x≠0）
（1）当m=1时，判断f（x）在（﹣∞，0）的单调性，并用定义证明；
（2）若对任意x∈（1，+∞），不等式 f（log2x）＞0恒成立，求m的取值范围．
（3）讨论f（x）零点的个数．

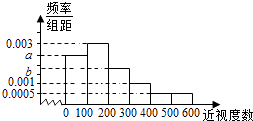
将近视程度由低到高分为4个等级：当近视度数在0﹣100时，称为不近视，记作0；当近视度数在100﹣200时，称为轻度近视，记作1；当近视度数在200﹣400时，称为中度近视，记作2；当近视度数在400以上时，称为高度近视，记作3．
（1）从该校任选1名高二学生，估计该生近视程度未达到中度及以上的概率；
（2）设a=0.0024，从该校任选1名高三学生，估计该生近视程度达到中度或中度以上的概率；
（3）把频率近似地看成概率，用随机变量X，Y分别表示高二、高三年级学生的近视程度，若EX=EY，求b．