
科目: 来源: 题型:
【题目】某体育场要建造一个长方形游泳池,其容积为4800m3 , 深为3m,如果建造池壁的单价为a且建造池底的单价是建造池壁的1.5倍,怎样设计水池的长和宽,才能使总造价最底?最低造价是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图是函数y=f(x)的导函数y=f′(x)的图象,给出下列命题: ①﹣3是函数y=f(x)的极值点;
②﹣1是函数y=f(x)的最小值点;
③y=f(x)在x=0处切线的斜率小于零;
④y=f(x)在区间(﹣3,1)上单调递增.
则正确命题的序号是 . 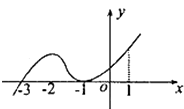
查看答案和解析>>
科目: 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2
(t为参数),以原点为极点,x轴正半轴为极轴建立极坐标系,⊙C的极坐标方程为ρ=2 ![]() sinθ. (Ⅰ)写出⊙C的直角坐标方程;
sinθ. (Ⅰ)写出⊙C的直角坐标方程;
(Ⅱ)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ex , g(x)=mx2+ax+b,其中m,a,b∈R,e=2.71828…为自然对数的底数. (I)函数h(x)=xf (x),当a=l,b=0时,若函数h(x)与g(x)具有相同的单调区间,求m的值;
(II)记F(x)=f(x)﹣g(x).当a=2,m=0时,若函数F(x)在[﹣1,2]上存在两个不同的零点,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的焦距为4
=1(a>b>0)的焦距为4 ![]() ,且椭圆C过点(2
,且椭圆C过点(2 ![]() ,1). (Ⅰ)求椭圆C的方程;
,1). (Ⅰ)求椭圆C的方程;
(Ⅱ)设椭圆C与y轴负半轴的交点为B,如果直线y=kx+1(k≠0)交椭圆C于不同的两点E、F,且B,E,F构成以EF为底边,B为顶点的等腰三角形,判断直线EF与圆x2+y2= ![]() 的位置关系.
的位置关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,直四棱柱ABCD﹣A1B1C1D1中,AB∥CD,AD⊥AB,AB=2,AD= ![]() ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3 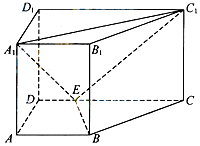
(1)证明:BE⊥平面BB1C1C;
(2)求三棱锥B1﹣EA1C1的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com