A. 如果平面平面，那么平面内一定存在直线平行于平面

B. 如果平面不垂直平面，那么平面内一定不存在直线垂直于平面

C. 如果平面平面，平面平面，且，那么

D. 如果平面平面，那么平面内所有直线都垂直于平面

(1)求f(x)的解析式；

(2)若f(x)在区间[2a，a＋1]上不单调，求实数a的取值范围；

(3)在区间[－1,1]上，y＝f(x)的图象恒在y＝2x＋2m＋1的图象上方，试确定实数m的范围．

【题目】定义在上的函数，如果满足：对任意，存在常数，都有成立，则称是上的有界函数，其中称为函数的上界．

（）判断函数， 是否是有界函数，请写出详细判断过程．

（）试证明：设， ，若， 在上分别以， 为上界，求证：函数在上以为上界．

（）若函数在上是以为上界的有界函数，求实数的取值范围．

(1)DF⊥AP.

(2)在线段AD上是否存在点G，使GF⊥平面PBC？若存在，说明G点的位置，并证明你的结论；若不存在，说明理由．

【题目】已知函数f（x）= x3﹣4x+4，
（1）求f（x）的单调区间；
（2）求f（x）在[0，3]上的最大值和最小值．

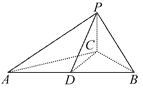
(1)求证：平面PAC⊥平面ABC.

(2)求二面角D-AP-C的正弦值.

【题目】已知函数f（x）=x3+ax2+bx+c，x∈[﹣2，2]表示的曲线过原点，且在x=±1处的切线斜率均为﹣1，给出以下结论： ①f（x）的解析式为f（x）=x3﹣4x，x∈[﹣2，2]；
②f（x）的极值点有且仅有一个；
③f（x）的最大值与最小值之和等于0．
其中正确的结论有（ ）
A.0个
B.1个
C.2个
D.3个

【题目】如图所示，平面ABCD⊥平面ABEF，四边形ABCD是正方形，四边形ABEF是矩形，AF＝AD＝a，G是EF的中点．

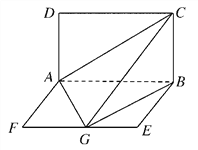
(1)求证：平面AGC⊥平面BGC；

(2)求GB与平面AGC所成角的正弦值．

【题目】一同学在电脑中打出如下若干个圈：○●○○●○○○●○○○○●○○○○○●…若将此若干个圈依此规律继续下去，得到一系列的圈，那么在前55个圈中的●的个数是（ ）
A.10
B.9
C.8
D.11

【题目】已知函数f（x）=ax+ ，其中函数f（x）的图象在点（1，f（1））处的切线方程为y=x﹣1．
（1）若a= ，求函数f（x）的解析式；
（2）若f（x）≥g（x）在[1，+∞）上恒成立，求实数a的取值范围；
（3）证明：1+ ．