【题目】现有某批次同一型号的产品共10件，其中有8件合格品，2件次品．
（Ⅰ）某检验员从中有放回地连续抽取产品2次，每次随机抽取1件，求两次都取到次品的概率；
（Ⅱ）若该检验员从中任意抽取2件，用X表示取出的2件产品中次品的件数，求X的分布列．

【题目】某企业有甲、乙两个研发小组，他们研发新产品成功的概率分别为 和 ．现安排甲组研发新产品A，乙组研发新产品B，设甲、乙两组的研发相互独立．
（Ⅰ）求至少有一种新产品研发成功的概率；
（Ⅱ）若新产品A研发成功，预计企业可获利润120万元；若新产品B研发成功，预计企业可获利润100万元，求该企业可获利润的分布列和数学期望．

【题目】某厂生产一种产品的固定成本(即固定投入)为0.5万元,但每生产一百件这样的产品,需要增加可变成本(即另增加投入)0.25万元. 市场对此产品的年需求量为500件,销售的收入函数为= (单位:万元),其中是产品售出的数量(单位:百件).

(1)该公司这种产品的年产量为百件,生产并销售这种产品所得到的利润为当年产量的函数,求;

(2)当年产量是多少时,工厂所得利润最大?

【题目】设函数f（x）= ，g（x）=a（x+b）（0＜a≤1，b≤0）．
（1）讨论函数y=f（x）g（x）的奇偶性；
（2）当b=0时，判断函数y= 在（﹣1，1）上的单调性，并说明理由；
（3）设h（x）=|af2（x）﹣ |，若h（x）的最大值为2，求a+b的取值范围．

(1)求f(x)的解析式;

(2)当x∈[t,t+2],t∈R时,求函数f(x)的最小值(用t表示).

【题目】如图，P是直线x=4上一动点，以P为圆心的圆Γ经定点B（1，0），直线l是圆Γ在点B处的切线，过A（﹣1，0）作圆Γ的两条切线分别与l交于E，F两点．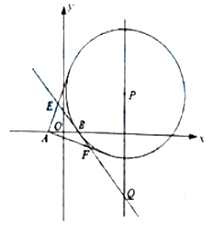
（1）求证：|EA|+|EB|为定值；
（2）证明：设直线l交直线x=4于点Q，证明：|EB||FQ|=|BF|EQ|．

【题目】一个圆柱形圆木的底面半径为1 m，长为10 m，将此圆木沿轴所在的平面剖成两部分．现要把其中一部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形ABCD（如图所示，其中O为圆心，C，D在半圆上），设，木梁的体积为V（单位：m3），表面积为S（单位：m2）．

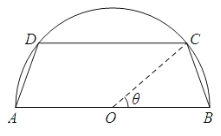
（1）求V关于θ的函数表达式；

（2）求的值，使体积V最大；

（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．

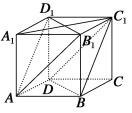
（1）求证：平面AB1D1∥平面C1BD；

（2）试找出体对角线A1C与平面AB1D1和平面C1BD的交点E，F，并证明：A1E＝EF＝FC.