【题目】如图， 是圆柱的母线， 是的直径， 是底面圆周上异于的任意一点， ， .

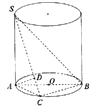
（1）求证：

（2）当三棱锥的体积最大时，求与平面所成角的大小；

（3）上是否存在一点，使二面角的平面角为45°？若存在，求出此时的长；若不存在，请说明理由.

【题目】如图，在三棱锥中，平面平面， 为等边三角形， 且， 分别为的中点.

（1）求证： 平面.

（2）求证：平面平面.

（3）求三棱锥的体积.

【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为

（1）求频率分布图中的值，并估计该企业的职工对该部门评分不低于80的概率；

（2）从评分在的受访职工中，随机抽取2人，求此2人评分都在的概率．．

【题目】已知函数， ．

（1）设 ，若是偶函数，求实数的值；

（2）设，求函数在区间上的值域；

（3）若不等式恒成立，求实数的取值范围.

【题目】给出下面三个类比结论：
①向量 ，有| |2= 2；类比复数z，有|z|2=z2
②实数a，b有（a+b）2=a2+2ab+b2；类比向量 ， ，有（ ）2= 2 2
③实数a，b有a2+b2=0，则a=b=0；类比复数z1 ， z2 ， 有z12+z22=0，则z1=z2=0
其中类比结论正确的命题个数为（ ）
A.0
B.1
C.2
D.3

【题目】已知函数 ，且满足.

（1）判断函数在上的单调性，并用定义证明；

（2）设函数，求在区间上的最大值；

（3）若存在实数m，使得关于x的方程恰有4个不同的正根，求实数m的取值范围.

【题目】已知圆M： 和点 ，动圆P经过点N且与圆M相切，圆心P的轨迹为曲线E．
（1）求曲线E的方程；
（2）点A是曲线E与x轴正半轴的交点，点B，C在曲线E上，若直线AB，AC的斜率分别是k1 ， k2 ， 满足k1k2=9，求△ABC面积的最大值．

【题目】过点（0，2）的直线l与中心在原点，焦点在x轴上且离心率为 的椭圆C相交于A、B两点，直线 过线段AB的中点，同时椭圆C上存在一点与右焦点关于直线l对称．
（1）求直线l的方程；
（2）求椭圆C的方程．

【题目】为迎接2017年“双11”，“双12”购物狂欢节的来临，某青花瓷生产厂家计划每天生产汤碗、花瓶、茶杯这三种瓷器共100个，生产一个汤碗需5分钟，生产一个花瓶需7分钟，生产一个茶杯需4分钟，已知总生产时间不超过10小时．若生产一个汤碗可获利润5元，生产一个花瓶可获利润6元，生产一个茶杯可获利润3元．
（1）使用每天生产的汤碗个数x与花瓶个数y表示每天的利润ω（元）；
（2）怎样分配生产任务才能使每天的利润最大，最大利润是多少？

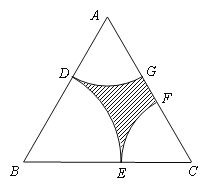
【题目】近年来，随着我市经济的快速发展，政府对民生也越来越关注. 市区现有一块近似正三角形土地ABC（如图所示），其边长为2百米，为了满足市民的休闲需求，市政府拟在三个顶点处分别修建扇形广场，即扇形DBE，DAG和ECF，其中、与分别相切于点D、E，且与无重叠，剩余部分（阴影部分）种植草坪. 设BD长为x（单位：百米），草坪面积为S（单位：百米2）.

（1）试用x分别表示扇形DAG和DBE的面积，并写出x的取值范围；

（2）当x为何值时，草坪面积最大？并求出最大面积.