【题目】在△ABC中，∠A，∠B，∠C的对边分别为, , ，若,

(1)求∠B的大小；

(2)若， ，求△ABC的面积．

【题目】已知函数， 且.

(1)判断的奇偶性并予以证明；

(2)当时，求使的的解集.

【题目】选修4-4：坐标系与参数方程
在平面直角坐标系xoy中，直线l的参数方程为 （t为参数， ），以坐标原点o为极点，x轴的正半轴为极轴，并取相同的长度单位，建立极坐标系.曲线
（1）若直线l曲线 相交于点 ， ， ，证明： 为定值；
（2）将曲线 上的任意点 作伸缩变换 后，得到曲线 上的点 ，求曲线 的内接矩形 周长的最大值.

【题目】已知定义域为的函数是奇函数.

(1)求的值；

(2)判断函数的单调性并证明；

(2)若关于的不等式在有解，求实数的取值范围.

【题目】已知圆M：与轴相切．

(1)求的值；

(2)求圆M在轴上截得的弦长；

(3)若点是直线上的动点，过点作直线与圆M相切，为切点，求四边形面积的最小值．

【答案】(1) (2) (3)

【解析】试题分析：(1)先将圆的一般方程化成标准方程，利用直线和圆相切进行求解；(2) 令，得到关于的一元二次方程进行求解；(3)将四边形的面积的最小值问题转化为点到直线的的距离进行求解.

试题解析：(1) 　　∵圆M：与轴相切　　

∴　　　∴

(2) 令，则　　∴

　∴

(3)

　∵的最小值等于点到直线的距离，　

∴　∴

∴四边形面积的最小值为．

【题型】解答题
【结束】
20

【题目】在平面直角坐标系中，圆的方程为，且圆与轴交于， 两点，设直线的方程为．

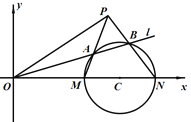
（1）当直线与圆相切时，求直线的方程；

（2）已知直线与圆相交于， 两点．

（ⅰ）若，求实数的取值范围；

（ⅱ）直线与直线相交于点，直线，直线，直线的斜率分别为， ， ，

是否存在常数，使得恒成立？若存在，求出的值；若不存在，说明理由．

【题目】在数列{an}中，an=cos （n∈N*）
（1）试将an+1表示为an的函数关系式；
（2）若数列{bn}满足bn=1﹣ （n∈N*），猜想an与bn的大小关系，并证明你的结论．

【题目】已知直线l：x－2y＋2m－2＝0．

(1)求过点(2，3)且与直线l垂直的直线的方程；

(2)若直线l与两坐标轴所围成的三角形的面积大于4，求实数m的取值范围．

【答案】（1）；（2）

【解析】试题分析：（1）由直线的斜率为，可得所求直线的斜率为，代入点斜式方程，可得答案；（2）直线与两坐标轴的交点分别为，则所围成的三角形的面积为，根据直线与两坐标轴所围成的三角形的面积为大于，构造不等式，解得答案.

试题解析：(1)与直线l垂直的直线的斜率为－2，

因为点(2，3)在该直线上，所以所求直线方程为y－3＝－2(x－2)，

故所求的直线方程为2x＋y－7＝0．

(2) 直线l与两坐标轴的交点分别为(－2m＋2，0)，(0，m－1)，

则所围成的三角形的面积为×|－2m＋2|×|m－1|．

由题意可知×|－2m＋2|×|m－1|＞4，化简得(m－1)2＞4，

解得m＞3或m＜－1，

所以实数m的取值范围是(－∞，－1)∪(3，＋∞)．

【方法点睛】本题主要考查直线的方程，两条直线平行与斜率的关系，属于简单题. 对直线位置关系的考查是热点命题方向之一，这类问题以简单题为主，主要考查两直线垂直与两直线平行两种特殊关系：在斜率存在的前提下，（1） ；（2），这类问题尽管简单却容易出错，特别是容易遗忘斜率不存在的情况，这一点一定不能掉以轻心.

【题型】解答题
【结束】
18

【题目】在平面直角坐标系中，已知经过原点O的直线与圆交于两点。

（1）若直线与圆相切，切点为B，求直线的方程；

（2）若，求直线的方程；

【题目】某校举办校园科技文化艺术节，在同一时间安排《生活趣味数学》和《校园舞蹈赏析》两场讲座．已知A、B两学习小组各有5位同学，每位同学在两场讲座任意选听一场．若A组1人选听《生活趣味数学》，其余4人选听《校园舞蹈赏析》；B组2人选听《生活趣味数学》，其余3人选听《校园舞蹈赏析》．
（1）若从此10人中任意选出3人，求选出的3人中恰有2人选听《校园舞蹈赏析》的概率；
（2）若从A、B两组中各任选2人，设X为选出的4人中选听《生活趣味数学》的人数，求X的分布列和数学期望E（X）．

【题目】在平面直角坐标系xOy中，已知△ABC三个顶点坐标为A(7，8)，B(10，4)，C(2，－4)．

(1)求BC边上的中线所在直线的方程；

(2)求BC边上的高所在直线的方程．

【答案】（1）；（2）

【解析】试题分析：（1）根据中点坐标公式求出中点的坐标，根据斜率公式可求得的斜率，利用点斜式可求边上的中线所在直线的方程；（2）先根据斜率公式求出的斜率，从而求出边上的高所在直线的斜率为，利用点斜式可求边上的高所在直线的方程.

试题解析：（1）由B(10，4)，C(2，－4)，得BC中点D的坐标为（6，0），

所以AD的斜率为k＝＝8，

所以BC边上的中线AD所在直线的方程为y－0＝8(x－6)，

即8x－y－48＝0．

（2）由B(10，4)，C(2，－4)，得BC所在直线的斜率为k＝＝1，

所以BC边上的高所在直线的斜率为－1，

所以BC边上的高所在直线的方程为y－8＝－(x－7)，即x＋y－15＝0．

【题型】解答题
【结束】
17

(1)求过点(2，3)且与直线l垂直的直线的方程；

(2)若直线l与两坐标轴所围成的三角形的面积大于4，求实数m的取值范围．