【题目】已知 在椭圆C： 上，F为右焦点，PF⊥垂直于x轴，A，B，C，D为椭圆上的四个动点，且AC，BD交于原点O．
（1）求椭圆C的方程；
（2）判断直线l： 与椭圆的位置关系；
（3）设A（x1 ， y1），B（x2 ， y2）满足 = ，判断kAB+kBC的值是否为定值，若是，请求出此定值，并求出四边形ABCD面积的最大值，否则说明理由．

【题目】若函数为定义域上的单调函数，且存在区间(其中，使得当时，的取值范围恰为,则称函数是上的正函数，区间叫做函数的等域区间．

（1）已知是上的正函数,求的等域区间；

（2）试探求是否存在，使得函数是上的正函数？若存在，请求出实数的取值范围；若不存在，请说明理由．

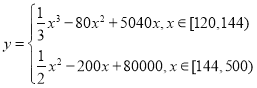为了保护环境，发展低碳经济，某单位在政府部门的支持下，进行技术攻关，采用了新工艺，新上了把二氧化碳转化为一种可利用的化工产品的项目.经测算，月处理成本（元）与月处理量（吨）之间的函数关系可以近似的表示为：，且每处理一吨二氧化碳可得到能利用的化工产品价值为200元，若该项目不获利，政府将补贴.

（I）当时，判断该项目能否获利？如果获利，求出最大利润；如果不获利，则政府每月至少需要补贴多少元才能使该项目不亏损；

（II）该项目每月处理量为多少吨时，才能使每吨的平均处理成本最低？

【题目】已知f（x）=ax3﹣x2﹣x+b（a，b∈R，a≠0），g（x）= （e是自然对数的底数），f（x）的图象在x=﹣ 处的切线方程为y= ．
（1）求a，b的值；
（2）探究直线y= ．是否可以与函数g（x）的图象相切？若可以，写出切点的坐标，否则，说明理由；
（3）证明：当x∈（﹣∞，2]时，f（x）≤g（x）．

【题目】如图所示,直角梯形ACDE与等腰直角三角形ABC所在平面互相垂直,F为BC的中点,, ,.

(1)求证:平面平面;

(2)求证:平面.

【题目】平面直角坐标系xoy中，直线l的参数方程是 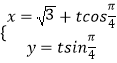（t为参数），以射线ox为极轴建立极坐标系，曲线C的极坐标方程是 +ρ2sin2θ=1．
（1）求曲线C的直角坐标方程；
（2）求直线l与曲线C相交所得的弦AB的长．

【题目】已知三棱锥 ，底面 是以 为直角顶点的等腰直角三角形， ， ，二面角 的大小为 .

（1）求直线 与平面 所成角的大小；
（2）求二面角 的正切值.

【题目】已知函数f（x）= ．
（1）证明：f（x）+|f（x）﹣2|≥2；
（2）当x≠﹣1时，求y= 的最小值．

根据上表可得回归直线方程 ，其中 ，据此估计，该社区一户购买食品的年支出费用为3.00万元的家庭购买水果和牛奶的年支出费用约为（ ）
A.1.79万元
B.2.55万元
C.1.91万元
D.1.94万元

【题目】已知椭圆 的离心率为 ，且它的一个焦点 的坐标为 .
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设过焦点 的直线与椭圆相交于 两点， 是椭圆上不同于 的动点，试求 的面积的最大值.