【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准（吨）、一位居民的月用水量不超过的部分按平价收费，超出的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0,0.5)，[0.5,1)，…，[4,4.5)分成9组，制成了如图所示的频率分布直方图.

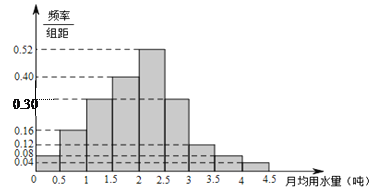
（1）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；

（2）若该市政府希望使85%的居民每月的用水量不超过标准（吨），估计的值，并说明理由.

（3）利用分层抽样的方法在[0,0.5) [3.5,4) [4,4.5)三组中选取5位居民，再从这5位居民中任意取三人，求这三人恰有两人来自同一组的概率。

(1)求{an}的通项公式．

(2)设等比数列{bn}满足b2＝a3，b3＝a7.问：b6与数列{an}的第几项相等？

【题目】设，满足：，则的从小到大顺序为____．

【题目】已知函数 .
（1）求 的单调区间；
（2）若 对一切 恒成立，求 的取值范围.

【题目】已知由实数组成的等比数列{an}的前项和为Sn ， 且满足8a4=a7 ， S7=254．
（1）求数列{an}的通项公式；
（2）对n∈N* ， bn= ，求数列{bn}的前n项和Tn ．

【题目】利用随机模拟的方法可以估计图中由曲线与两直线x=2及y=0所围成的阴影部分的面积S：①先产生两组0～1的均匀随机数，a=RAND（　），b=RAND（　）；② 做变换，令x=2a，y=2b；③产生N个点（x，y），并统计落在阴影内的点（x，y）的个数，已知某同学用计算机做模拟试验结果，选取了以下20组数据（如图所示），则据此可估计S的值为____．

【题目】已知抛物线 ，直线 与 交于 ， 两点，且 ，其中 为坐标原点.
（1）求抛物线 的方程；
（2）已知点 的坐标为（-3,0），记直线 、 的斜率分别为 ， ，证明： 为定值.

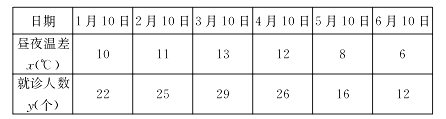
【题目】某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系，他们分别到气象局与某医院抄录了1至6月每月10号的昼夜温差情况与因患感冒而就诊的人数，得到如下的资料：
该兴趣小组确定的研究方案是：现从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选用的2组数据进行检验.
参考公式：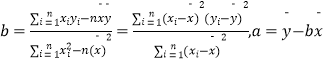


（1）求选取的2组数据恰好是相邻两个月的概率；
（2）若选取的是1月与6月的两组数据，请根据2至5月的数据，求出 关于 的线性回归方程 ；
（3）若有线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人，则认为得到的线性回归方程是理想的，试问（2）中所得线性回归方程是否是理想？

【题目】如图所示的几何体 为一简单组合体，在底面 中， ， ， ， 平面 ， ， ， ．

（1）求证：平面 平面 ；
（2）求该组合体 的体积．

（Ⅰ）若a＝5，b＝3，k＝2，求事件A发生的概率；

（Ⅱ）判断事件B发生的概率是否随k取值的变化而变化？并说明理由；

（Ⅲ）比较a＝5，b＝9时事件A发生的概率与a＝5，b＝10时事件A发生的概率的大小，并说明理由。