
科目: 来源: 题型:
【题目】如图,在直角坐标系![]() 中,椭圆
中,椭圆![]() 的上焦点为
的上焦点为![]() ,椭圆
,椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点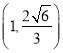 .
.
(1)求椭圆![]() 的方程.
的方程.
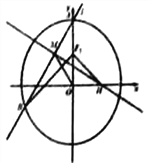
(2)设过椭圆![]() 的上顶点
的上顶点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目: 来源: 题型:
【题目】共享单车进驻城市,绿色出行引领时尚.某市有统计数据显示,2017年该市共享单车用户年龄登记分布如图1所示,一周内市民使用单车的频率分布扇形图如图2所示.若将共享单车用户按照年龄分为“年轻人”(20岁至39岁)和“非年轻人”(19岁及以下或者40岁及以上)两类,将一周内使用的次数为6次或6次以上的称为“经常使用单车用户”,使用次数为5次或不足5次的称为“不常使用单车用户”.已知在“经常使用单车用户”中有![]() 是“年轻人”.
是“年轻人”.

(1)现对该市市民进行“经常使用共享单车与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为200的样本,请你根据图表中的数据,补全下列![]() 列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?
列联表,并根据列联表的独立性检验,判断能有多大把握可以认为经常使用共享单车与年龄有关?

(2)将频率视为概率,若从该市市民中随机任取3人,设其中经常使用共享单车的“非年轻人”人数为随机变量![]() ,求
,求![]() 的分布与期望.
的分布与期望.
(参考数据:独立性检验界值表 ,其中
,其中![]() )
)

查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量![]() ,
, ![]() .
.
(1)若![]() 分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足
分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6),先后抛掷两次时第一次、第二次出现的点数,求满足![]() 的概率;
的概率;
(2)若![]() 在连续区间
在连续区间![]() 上取值,求满足
上取值,求满足![]() 的概率.
的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :关于
:关于![]() 的方程
的方程![]() 有实根.
有实根.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围.
的取值范围.
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

查看答案和解析>>
科目: 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60 min的学生称为“书虫”,低于60 min的学生称为“懒虫”,

(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)
(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:

查看答案和解析>>
科目: 来源: 题型:
【题目】某单位N名员工参加“社区低碳你我他”活动,他们的年龄在25岁至50岁之间。按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。
,由统计的数据得到的频率分布直方图如图所示,下表是年龄的频率分布表。

区间 |
|
|
|
|
|
人数 |
| a | b |
(1)求正整数a,b,N的值;
(2)现要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,则年龄在第1,2,3组中抽取的人数分别是多少?
(3)在(2)的条件下,从这6人中随机抽取2人参加社区宣传交流活动,求恰有1 人在第3组的概率。
查看答案和解析>>
科目: 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得![]() =80,
=80, ![]() =20,
=20, ![]() =184,
=184, ![]() =720.
=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中,  ,a=
,a=![]() -b
-b![]() ,其中
,其中![]() ,
, ![]() 为样本平均值.
为样本平均值.
查看答案和解析>>
科目: 来源: 题型:
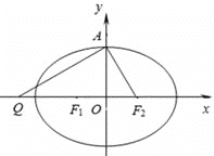
【题目】设椭圆![]() :
: ![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,上顶点为A,过点A与
,上顶点为A,过点A与![]() 垂直的直线交
垂直的直线交![]() 轴负半轴于点
轴负半轴于点![]() ,且
,且![]() ,若过
,若过![]() ,
, ![]() ,
, ![]() 三点的圆恰好与直线
三点的圆恰好与直线![]() 相切.过定点
相切.过定点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点(点
两点(点![]() 在点
在点![]() ,
, ![]() 之间).
之间).
(Ⅰ)求椭圆![]() 的方程;(Ⅱ)若实数
的方程;(Ⅱ)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com