
科目: 来源: 题型:
【题目】设椭圆 ![]() 1(a>
1(a> ![]() )的右焦点为F,右顶点为A,已知
)的右焦点为F,右顶点为A,已知 ![]() ,其中O为原点,e为椭圆的离心率.
,其中O为原点,e为椭圆的离心率.
(1)求椭圆的方程;
(2)设过点A的直线l与椭圆交于B(B不在x轴上),垂直于l的直线与l交于点M,与y轴交于点H,若BF⊥HF,且∠MOA=∠MAO,求直线l的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图. 图中A点表示十月的平均最高气温约为![]() ,B点表示四月的平均最低气温约为
,B点表示四月的平均最低气温约为![]() . 下面叙述不正确的是 ( )
. 下面叙述不正确的是 ( )

A. 各月的平均最低气温都在![]() 以上
以上
B. 七月的平均温差比一月的平均温差大
C. 三月和十一月的平均最高气温基本相同
D. 平均最高气温高于![]() 的月份有5个
的月份有5个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知向量a=(![]() cos ωx,1),b=
cos ωx,1),b=![]() ,函数f(x)=a·b,且f(x)图象的一条对称轴为x=
,函数f(x)=a·b,且f(x)图象的一条对称轴为x=![]() .
.
(1)求f![]() 的值;
的值;
(2)若f![]() ,f
,f![]() ,且α,β∈
,且α,β∈![]() ,求cos(α-β)的值.
,求cos(α-β)的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R。
(1)求f(x)的单调区间;
(2)若f(x)存在极点x0 , 且f(x1)=f(x0),其中x1≠x0 , 求证:x1+2x0=3;
(3)设a>0,函数g(x)=∣f(x)∣,求证:g(x)在区间[0,2]上的最大值不小于 ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的中心为O , 四边形OBEF为矩形,平面OBEF⊥平面ABCD , 点G为AB的中点,AB=BE=2.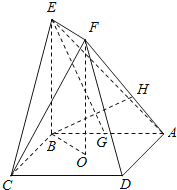
(1)求证:EG∥平面ADF;
(2)求二面角O-EF-C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF , 求直线BH和平面CEF所成角的正弦值.
HF , 求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=Asin![]()
(A>0,ω>0)的最小值为-2,其图象相邻两个对称中心之间的距离为![]() .
.
(1)求f(x)的最小正周期及对称轴方程;
(2)若f![]() ,求f
,求f![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=cos4x+sin2x,下列结论中错误的是( )
A. f(x)是偶函数
B. 函数f(x)最小值为![]()
C. ![]() 是函数f(x)的一个周期
是函数f(x)的一个周期
D. 函数f(x)在![]() 内是减函数
内是减函数
查看答案和解析>>
科目: 来源: 题型:
【题目】已知斜三棱柱![]() 的底面是直角三角形,
的底面是直角三角形,![]() ,侧棱与底面成锐角
,侧棱与底面成锐角![]() ,点
,点![]() 在底面上的射影
在底面上的射影![]() 落在
落在![]() 边上.
边上.

(Ⅰ) 求证:![]() 平面
平面![]() ;
;
(Ⅱ) 当![]() 为何值时,
为何值时,![]() ,且
,且![]() 为
为![]() 的中点?
的中点?
(Ⅲ) 当![]() ,且
,且![]() 为
为![]() 的中点时,若
的中点时,若![]() ,四棱锥
,四棱锥![]() 的体积为
的体积为![]() ,求二面角
,求二面角![]() 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com