
科目: 来源: 题型:
【题目】如图,在△ABC中,已知CA=1,CB=2,∠ACB=60°.

(1)求|![]() |;
|;
(2)已知点D是AB上一点,满足![]() =λ
=λ![]() ,点E是边CB上一点,满足
,点E是边CB上一点,满足![]() =λ
=λ![]() .
.
①当λ=![]() 时,求
时,求![]()
![]() ;
;
②是否存在非零实数λ,使得![]() ⊥
⊥![]() ?若存在,求出的λ值;若不存在,请说明理由.
?若存在,求出的λ值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
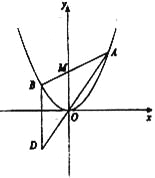
【题目】如图所示,已知抛物线![]() ,过点
,过点![]() 任作一直线与
任作一直线与![]() 相交于
相交于![]() 两点,过点
两点,过点![]() 作
作![]() 轴的平行线与直线
轴的平行线与直线![]() 相交于点
相交于点![]() 为坐标原点).
为坐标原点).
(1)证明: 动点![]() 在定直线上;
在定直线上;
(2)作![]() 的任意一条切线
的任意一条切线![]() (不含
(不含![]() 轴), 与直线
轴), 与直线![]() 相交于点
相交于点![]() 与(1)中的定直线相交于点
与(1)中的定直线相交于点![]() .
.
证明: ![]() 为定值, 并求此定值.
为定值, 并求此定值.
查看答案和解析>>
科目: 来源: 题型:
【题目】以原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的方程为 ![]() ,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
,⊙C的极坐标方程为ρ=4cosθ+2sinθ.
(1)求直线l和⊙C的普通方程;
(2)若直线l与圆⊙C交于A,B两点,求弦AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】解答题
(1)求函数f(x)=xlnx﹣(1﹣x)ln(1﹣x)在0<x≤ ![]() 上的最大值;
上的最大值;
(2)证明:不等式x1﹣x+(1﹣x)x≤ ![]() 在(0,1)上恒成立.
在(0,1)上恒成立.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆Г: ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 离心率为
(a>b>0)的左、右焦点分别为F1 , F2 , 离心率为 ![]() ,F2与椭圆上点的连线的中最短线段的长为
,F2与椭圆上点的连线的中最短线段的长为 ![]() ﹣1.
﹣1.
(1)求椭圆Г的标准方程;
(2)已知Г上存在一点P,使得直线PF1 , PF2分别交椭圆Г于A,B,若 ![]() =2
=2 ![]() ,
, ![]() =λ
=λ ![]() (λ>0),求λ的值.
(λ>0),求λ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某企业有甲、乙两个研发小组,他们研究新产品成功的概率分别为 ![]() 和
和 ![]() ,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
,现安排甲组研发新产品A,乙组研发新产品B,设甲、乙两组的研发相互独立.
(1)求恰好有一种新产品研发成功的概率;
(2)若新产品A研发成功,预计企业可获得利润120万元,不成功则会亏损50万元;若新产品B研发成功,企业可获得利润100万元,不成功则会亏损40万元,求该企业获利ξ万元的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知两条直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0. 求满足下列条件的a,b值.
(Ⅰ)l1⊥l2且l1过点(﹣3,﹣1);
(Ⅱ)l1∥l2且原点到这两直线的距离相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在三棱柱ABC﹣A1B1C1中,AB⊥平面BB1C1C,∠BCC1= ![]() ,AB=BB1=2,BC=1,D为CC1中点.
,AB=BB1=2,BC=1,D为CC1中点. 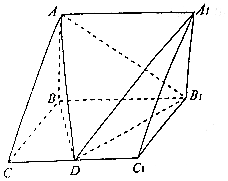
(1)求证:DB1⊥平面ABD;
(2)求二面角A﹣B1D﹣A1的平面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com