
科目: 来源: 题型:
【题目】已知二次函数f(x)的图象过点(0,4),对任意x满足f(3﹣x)=f(x),且f(1)=2.
(1)若f(x)在(a,2a﹣1)上单调递减,求实数a的取值范围.
(2)设函数h(x)=f(x)﹣(2t﹣3)x,其中t∈R,求h(x)在区间[0,1]上的最小值g (t).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知椭圆 ![]() +y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足
+y2=1,A,B,C,D为椭圆上四个动点,且AC,BD相交于原点O,设A(x1 , y1),B(x2 , y2)满足 ![]() =
= ![]() .
.
(1)求证: ![]() +
+ ![]() =
= ![]() ;
;
(2)kAB+kBC的值是否为定值,若是,请求出此定值,并求出四边形ABCD面积的最大值,否则,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,AA1=6,点E、F分别在棱BB1、CC1上,且BE= ![]() BB1 , C1F=
BB1 , C1F= ![]() CC1 .
CC1 . 
(1)求平面AEF与平面ABC所成角α的余弦值;
(2)若G为BC的中点,A1G与平面AEF交于H,且设 ![]() =
= ![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】设关于某产品的明星代言费x(百万元)和其销售额y(百万元),有如表的统计表格:
i | 1 | 2 | 3 | 4 | 5 | 合计 |
xi(百万元) | 1.26 | 1.44 | 1.59 | 1.71 | 1.82 | 7.82 |
wi(百万元) | 2.00 | 2.99 | 4.02 | 5.00 | 6.03 | 20.04 |
yi(百万元) | 3.20 | 4.80 | 6.50 | 7.50 | 8.00 | 30.00 |
| ||||||
其中 ![]() .
.
(1)在坐标系中,作出销售额y关于广告费x的回归方程的散点图,根据散点图指出:y=a+blnx,y=c+dx3哪一个适合作销售额y关于明星代言费x的回归类方程(不需要说明理由); 
(2)已知这种产品的纯收益z(百万元)与x,y有如下关系:x=0.2y﹣0.726x(x∈[1.00,2.00]),试写出z=f(x)的函数关系式,试估计当x取何值时,纯收益z取最大值?(以上计算过程中的数据统一保留到小数点第2位)
查看答案和解析>>
科目: 来源: 题型:
【题目】设数列{an}的前n项和是Sn , 若点An(n, ![]() )在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
)在函数f(x)=﹣x+c的图象上运动,其中c是与x无关的常数,且a1=3(n∈N*).
(1)求数列{an}的通项公式;
(2)记bn=a ![]() ,求数列{bn}的前n项和Tn的最小值.
,求数列{bn}的前n项和Tn的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在R上的函数f(x),满足当x>0时,f(x)>1,且对任意的x,y![]() ,有
,有![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)求证:对任意x![]() ,都有f(x)>0;
,都有f(x)>0;
(3)解不等式f(3![]() 2x)>4.
2x)>4.
查看答案和解析>>
科目: 来源: 题型:
【题目】微信支付诞生于微信红包,早期知识作为社交的一部分“发红包”而诞生的,在发红包之余才发现,原来微信支付不仅可以用来发红包,还可以用来支付,现在微信支付被越来越多的人们所接受,现从某市市民中随机抽取300为对是否使用微信支付进行调查,得到下列![]() 的列联表:
的列联表:
年轻人 | 非年轻人 | 总计 | |
经常使用微信支付 | 165 | 225 | |
不常使用微信支付 | |||
合计 | 90 | 300 |
根据表中数据,我们得到的统计学的结论是:由__________的把握认为“使用微信支付与年龄有关”。
|
|
|
|
|
|
|
|
|
|
|
|
其中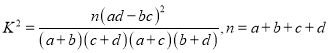
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com