
科目: 来源: 题型:
【题目】已知二次函数![]() .
.
(1)当q=1时,求f(x)在[﹣1,9]上的值域;
(2)问:是否存在常数q(0<q<10),使得当x∈[q,10]时,f(x)的最小值为﹣51?若存在,求出q的值,若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系xoy中,直线l的参数方程是 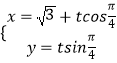 (t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是
(t为参数),以射线ox为极轴建立极坐标系,曲线C的极坐标方程是 ![]() +ρ2sin2θ=1.
+ρ2sin2θ=1.
(1)求曲线C的直角坐标方程;
(2)求直线l与曲线C相交所得的弦AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】下列有关命题的说法中错误的是
A. 在频率分布直方图中,中位数左边和右边的直方图的面积相等 .
B. 一个样本的方差是![]() ,则这组数据的总和等于60.
,则这组数据的总和等于60.
C. 在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越差.
D. 对于命题![]() 使得
使得![]() <0,则
<0,则![]() ,使
,使![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】(12分)已知函数f(x)对任意的实数m,n都有:f(m+n)=f(m)+f(n)-1,
且当x>0时,有f(x)>1.
(1)求f(0).
(2)求证:f(x)在R上为增函数.
(3)若f(1)=2,且关于x的不等式f(ax-2)+f(x-x2)<3对任意的x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知f(x)= ![]() ,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣
,g(x)=ax3﹣x2﹣x+b(a,b∈R,a≠0),g(x)的图象C在x=﹣ ![]() 处的切线方程是y=
处的切线方程是y= ![]() .
.
(1)若求a,b的值,并证明:当x∈(﹣∞,2]时,g(x)的图象C上任意一点都在切线y= ![]() 上或在其下方;
上或在其下方;
(2)求证:当x∈(﹣∞,2]时,f(x)≥g(x).
查看答案和解析>>
科目: 来源: 题型:
【题目】某市为了创建全国文明城市,面向社会招募志愿者,现从20岁至50岁的志愿者中按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
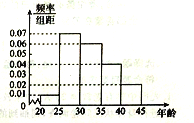
,第5组![]() ,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
,得到的频率分布直方图如图所示,若用分层抽样的方法从这些志愿者中抽取20人参加“创建全国文明城市验收日”的活动。
(1)求从第2组和第3组中抽取的人数分别是多少;
(2)若小李和小王都是32岁,同时参加了“创建全国文明城市验收日”的活动,现要从第3组抽取的人中临时抽调两人去执行另一任务,求小李和小王至少有一人被抽调的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com