
科目: 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,设倾斜角为
中,设倾斜角为![]() 的直线
的直线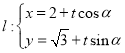 (
(![]() 为参数)与曲线
为参数)与曲线![]() (
(![]() 为参数)相交于不同的两点
为参数)相交于不同的两点![]() .
.
(1)若![]() ,求线段
,求线段![]() 中点
中点![]() 的坐标;
的坐标;
(2)若![]() ,其中
,其中![]() ,求直线
,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:圆心到直线的距离与圆的半径之比为直线关于圆的距离比![]() .
.
(1)设圆![]() 求过
求过![]() (2,0)的直线关于圆
(2,0)的直线关于圆![]() 的距离比
的距离比![]() 的直线方程;
的直线方程;
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() (0,3)且直线
(0,3)且直线![]() =
= ![]() 关于圆
关于圆![]() 的距离比
的距离比![]() ,求此圆的
,求此圆的![]() 的方程;
的方程;
(3)是否存在点![]() ,使过
,使过![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 的距离比始终相等?若存在,求出相应的点
的距离比始终相等?若存在,求出相应的点![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】从某学校高三年级共800名男生中随机抽取50名测量身高,测量发现被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160);第二组[160,165)、…、第八组[190,195],下图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组、第七组、第八组人数依次构成等差数列.
(1)估计这所学校高三年级全体男生身高180cm以上(含180cm)的人数;
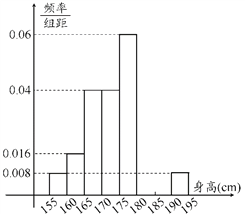
(2)求第六组、第七组的频率并补充完整频率分布直方图(如需增加刻度请在纵轴上标记出数据,并用直尺作图);
(3)由直方图估计男生身高的中位数.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上且满足下列两个条件:
上且满足下列两个条件:
①对任意![]() 都有
都有![]() ;
;
②当![]() 时,有
时,有![]() ,
,
(1)求![]() ,并证明函数
,并证明函数![]() 在
在![]() 上是奇函数;
上是奇函数;
(2)验证函数![]() 是否满足这些条件;
是否满足这些条件;
(3)若![]() ,试求函数
,试求函数![]() 的零点.
的零点.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
科目: 来源: 题型:
【题目】随着节假日外出旅游人数增多,倡导文明旅游的同时,生活垃圾处理也面临新的挑战,某海滨城市沿海有![]() 三个旅游景点,在岸边
三个旅游景点,在岸边![]() 两地的中点处设有一个垃圾回收站点
两地的中点处设有一个垃圾回收站点![]() (如图),
(如图),![]() 两地相距10
两地相距10![]() ,从回收站
,从回收站![]() 观望
观望![]() 地和
地和![]() 地所成的视角为
地所成的视角为![]() ,且
,且![]() ,设
,设![]() ;
;
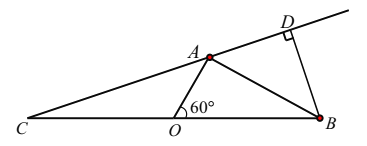
(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)某一时刻太阳与![]() 三点在同一直线,此时
三点在同一直线,此时![]() 地到直线
地到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】《最强大脑》是江苏卫视推出国内首档大型科学类真人秀电视节目,该节目集结了国内外最顶尖的脑力高手,堪称脑力界的奥林匹克,某校为了增强学生的记忆力和辨识力也组织了一场类似《最强大脑》的PK赛,A、B两队各由4名选手组成,每局两队各派一名选手PK,除第三局胜者得2分外,其余各局胜者均得1分,每局的负者得0分,假设每局比赛两队选手获胜的概率均为0.5,且各局比赛结果相互独立.
(1)求比赛结束时A队的得分高于B队的得分的概率;
(2)求比赛结束时B队得分X的分布列和期望.
查看答案和解析>>
科目: 来源: 题型:
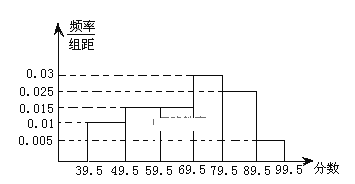
【题目】如图,从参加环保知识竞赛的学生中抽出![]() 名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
名,将其成绩(均为整数)整理后画出的频率分布直方图如下,观察图形,回答下列问题:
(1)![]() 这一组的频数、频率分别是多少?
这一组的频数、频率分别是多少?
(2)估计这次环保知识竞赛的及格率(![]() 分及以上为及格)和平均数?
分及以上为及格)和平均数?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1, ![]() ,
, ![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合,将矩形折叠,使
点与坐标原点重合,将矩形折叠,使![]() 点落在线段
点落在线段![]() 上,设此点为
上,设此点为![]() .
.
(1)若折痕的斜率为-1,求折痕所在的直线的方程;
(2)若折痕所在直线的斜率为![]() ,(
,( ![]() 为常数),试用
为常数),试用![]() 表示点
表示点![]() 的坐标,并求折痕所在的直线的方程;
的坐标,并求折痕所在的直线的方程;
(3)当![]() 时,求折痕长的最大值.
时,求折痕长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com