
科目: 来源: 题型:
【题目】如图,一个水轮的半径为4米,水轮圆心![]() 距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点
距离水面2米,已知水轮每分钟逆时针转动4圈,如果当水轮上点![]() 从水中浮现(图中点
从水中浮现(图中点![]() )开始计算时间.
)开始计算时间.
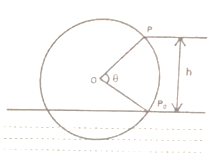
(1)将点![]() 距离水面的高度
距离水面的高度![]() (米)表示为时间
(米)表示为时间![]() (秒)的函数;
(秒)的函数;
(2)在水轮旋转一圈内,有多长时间点![]() 离开水面?
离开水面?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义域为{x|x≠0}的函数f(x)满足:f(xy)=f(x)f(y),f(x)>0且在区间(0,+∞)上单调递增,若m满足f(log3m)+f( ![]() )≤2f(1),则实数m的取值范围是( )
)≤2f(1),则实数m的取值范围是( )
A.[ ![]() ,1)∪(1,3]
,1)∪(1,3]
B.[0, ![]() )∪(1,3]
)∪(1,3]
C.(0, ![]() ]
]
D.[1,3]
查看答案和解析>>
科目: 来源: 题型:
【题目】直三棱柱ABC﹣A1B1C1中,∠BCA=90°,M、N分别是A1B1、A1C1的中点,BC=AC=CC1 , 则CN与AM所成角的余弦值等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】定义在R上的函数y=f(x).对任意的a,b∈R.满足:f(a+b)=f(a)f(b),当x>0时,有f(x)>1,其中f(1)=2.
(1)求f(0),f(﹣1)的值;
(2)判断该函数的单调性,并证明;
(3)求不等式f(x+1)<4的解集.
查看答案和解析>>
科目: 来源: 题型:
【题目】某粮库拟建一个储粮仓如图所示,其下部是高为2的圆柱,上部是母线长为2的圆锥,现要设计其底面半径和上部圆锥的高,若设圆锥的高![]() 为
为![]() ,储粮仓的体积为
,储粮仓的体积为![]() .
.
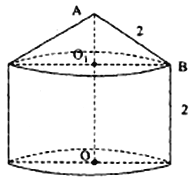
(1)求![]() 关于
关于![]() 的函数关系式;(圆周率用
的函数关系式;(圆周率用![]() 表示)
表示)
(2)求![]() 为何值时,储粮仓的体积最大.
为何值时,储粮仓的体积最大.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=log2x的定义域是[2,16].设g(x)=f(2x)﹣[f(x)]2.
(1)求函数g(x)的解析式及定义域;
(2)求函数g(x)的最值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=ax2+bx+c(a≠0),满足f(0)=2,f(x+1)﹣f(x)=2x﹣1
(1)求函数f(x)的解析式;
(2)当x∈[﹣1,2]时,求函数的最大值和最小值.
(3)若函数g(x)=f(x)﹣mx的两个零点分别在区间(﹣1,2)和(2,4)内,求m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】对于函数f(x)=(|x﹣2|+1)4,给出如下三个命题:①f(x+2)是偶函数;②f(x)在区间(﹣∞,2)上是减函数,在区间(2,+∞)上是增函数;③f(x)没有最小值.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com