【题目】已知.

（1）设， ，若函数存在零点，求的取值范围；

（2）若是偶函数，设，若函数与的图象只有一个公共点，求实数的取值范围.

【题目】设函数f（x）=ax2﹣a﹣lnx，其中a∈R．
（1）讨论f（x）的单调性；
（2）确定a的所有可能取值，使得f（x）＞ ﹣e1﹣x在区间（1，+∞）内恒成立（e=2.718…为自然对数的底数）．

【题目】食品安全问题越来越引起人们的重视，农药、化肥的滥用对人民群众的健康带来一定的危害，为了给消费者带来放心的蔬菜，某农村合作社每年投入200万元，搭建了甲、乙两个无公害蔬菜大棚，每个大棚至少要投入20万元，其中甲大棚种西红柿，乙大棚种黄瓜，根据以往的种菜经验，发现种西红柿的年收入种黄瓜的年收入与投入（单位：万元）满足.设甲大棚的投入为（单位：万元），每年两个大棚的总收益为（单位：万元）

（1）求的值；

（2）试问如何安排甲、乙两个大棚的投入，才能使总收益最大？

【题目】函数的部分图像如图所示，为最高点，该图像与轴交于点与轴交于点，且的面积为．

(1)求函数的解析式；

(2)将函数的图像向右平移个单位，再将所得图像上各点的横坐标伸长为原来的倍，纵坐标不变，得到函数的图像，求在上的单调递增区间。

【题目】如图，已知五面体，其中内接于圆，是圆的直径，四边形为平行四边形，且平面．

（1）证明：平面平面；

（2）若，，且二面角所成角的余弦值为，试求该几何体的体积．

【题目】已知椭圆E： =1（a＞b＞0）的两个焦点与短轴的一个端点是直角三角形的3个顶点，直线l：y=﹣x+3与椭圆E有且只有一个公共点T．
（1）求椭圆E的方程及点T的坐标；
（2）设O是坐标原点，直线l′平行于OT，与椭圆E交于不同的两点A、B，且与直线l交于点P．证明：存在常数λ，使得|PT|2=λ|PA||PB|，并求λ的值．

【题目】已知数列{an}的首项为1，Sn为数列{an}的前n项和，Sn+1=qSn+1，其中q＞0，n∈N* ．
（1）若2a2 ， a3 ， a2+2成等差数列，求an的通项公式；
（2）设双曲线x2﹣ =1的离心率为en ， 且e2= ，证明：e1+e2++en＞ ．

【题目】如图，在四棱锥P﹣ABCD中，AD∥BC，∠ADC=∠PAB=90°，BC=CD= AD．E为棱AD的中点，异面直线PA与CD所成的角为90°．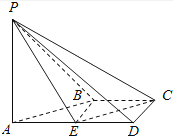
（1）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；
（2）若二面角P﹣CD﹣A的大小为45°，求直线PA与平面PCE所成角的正弦值．

【题目】在△ABC中，角A，B，C所对的边分别是a，b，c，且 + = ．
（1）证明：sinAsinB=sinC；
（2）若b2+c2﹣a2= bc，求tanB．

【题目】在平面直角坐标系xOy中，倾斜角为α的直线l的参数方程为(t为参数)．以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程是ρcos2θ－4sin θ＝0.

(1)写出直线l的普通方程和曲线C的直角坐标方程；

(2)已知点P(1,0)．若点M的极坐标为，直线l经过点M且与曲线C相交于A，B两点，设线段AB的中点为Q，求|PQ|的值．