
科目: 来源: 题型:
【题目】已知两条直线l1:ax﹣by+4=0,l2:(a﹣1)x+y+b=0. 求满足下列条件的a,b值.
(Ⅰ)l1⊥l2且l1过点(﹣3,﹣1);
(Ⅱ)l1∥l2且原点到这两直线的距离相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】某种新产品投放市场一段时间后,经过调研获得了时间![]() (天数)与销售单价
(天数)与销售单价![]() (元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
(元)的一组数据,且做了一定的数据处理(如表),并作出了散点图(如图)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
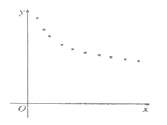
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作价格
哪一个更适宜作价格![]() 关于时间
关于时间![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若该产品的日销售量![]() (件)与时间
(件)与时间![]() 的函数关系为
的函数关系为![]() (
(![]() ),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
),求该产品投放市场第几天的销售额最高?最高为多少元?(结果保留整数)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为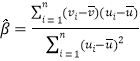 ,
,![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了![]() 名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.

(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有
列联表,并据此资料你是否有![]() 的把握认为选手成绩“优秀”与文化程度有关?
的把握认为选手成绩“优秀”与文化程度有关?
优秀 | 合格 | 合计 | |
大学组 | |||
中学组 | |||
合计 |
注:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
(2)若参赛选手共![]() 万人,用频率估计概率,试估计其中优秀等级的选手人数;
万人,用频率估计概率,试估计其中优秀等级的选手人数;
查看答案和解析>>
科目: 来源: 题型:
【题目】在下列命题中,①![]() 的一个充要条件是
的一个充要条件是![]() 与它的共轭复数相等:
与它的共轭复数相等:
②利用独立性检验来考查两个分类变量![]() ,
,![]() 是否有关系,当随机变量
是否有关系,当随机变量![]() 的观测值
的观测值![]() 值越大,“
值越大,“![]() 与
与![]() 有关系”成立的可能性越大;
有关系”成立的可能性越大;
③在回归分析模型中,若相关指数越大,则残差平方和越小,模型的拟合效果越好;
④若![]() ,
,![]() 是两个相等的实数,则
是两个相等的实数,则![]() 是纯虚数;
是纯虚数;
⑤某校高三共有![]() 个班,
个班,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,
人,![]() 班有
班有![]() 人,由此推测各班都超过
人,由此推测各班都超过![]() 人,这个推理过程是演绎推理.
人,这个推理过程是演绎推理.
其中真命题的序号为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在公园游园活动中有这样一个游戏项目:甲箱子里装有3个白球和2个黑球,乙箱子里装有1个白球和2个黑球,这些球除颜色外完全相同;每次游戏都从这两个箱子里各随机地摸出2个球,若摸出的白球不少于2个,则获奖.(每次游戏结束后将球放回原箱)
(1)在一次游戏中:①求摸出3个白球的概率;②求获奖的概率;
(2)在两次游戏中,记获奖次数为X:①求X的分布列;②求X的数学期望.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知函数f(x)=x﹣lnx,g(x)=x2﹣ax.
(1)求函数f(x)在区间[t,t+1](t>0)上的最小值m(t);
(2)令h(x)=g(x)﹣f(x),A(x1 , h(x1)),B(x2 , h(x2))(x1≠x2)是函数h(x)图象上任意两点,且满足 ![]() >1,求实数a的取值范围;
>1,求实数a的取值范围;
(3)若x∈(0,1],使f(x)≥ ![]() 成立,求实数a的最大值.
成立,求实数a的最大值.
查看答案和解析>>
科目: 来源: 题型:
【题目】一种药在病人血液中的含量不低于2克时,它才能起到有效治疗的作用,已知每服用![]() 且
且![]() 克的药剂,药剂在血液中的含量
克的药剂,药剂在血液中的含量![]() 克
克![]() 随着时间
随着时间![]() 小时
小时![]() 变化的函数关系式近似为
变化的函数关系式近似为![]() ,其中
,其中 .
.
![]() 若病人一次服用9克的药剂,则有效治疗时间可达多少小时?
若病人一次服用9克的药剂,则有效治疗时间可达多少小时?
![]() 若病人第一次服用6克的药剂,6个小时后再服用3m克的药剂,要使接下来的2小时中能够持续有效治疗,试求m的最小值.
若病人第一次服用6克的药剂,6个小时后再服用3m克的药剂,要使接下来的2小时中能够持续有效治疗,试求m的最小值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在数列{an}中,已知a1=2,an+1=3an+2n﹣1.
(1)求证:数列{an+n}为等比数列;
(2)记bn=an+(1﹣λ)n,且数列{bn}的前n项和为Tn , 若T3为数列{Tn}中的最小项,求λ的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某城市小区有一个矩形休闲广场,AB=20米,广场的一角是半径为16米的扇形BCE绿化区域,为了使小区居民能够更好的在广场休闲放松,现决定在广场上安置两排休闲椅,其中一排是穿越广场的双人靠背直排椅MN(宽度不计),点M在线段AD上,并且与曲线CE相切;另一排为单人弧形椅沿曲线CN(宽度不计)摆放.已知双人靠背直排椅的造价每米为2a元,单人弧形椅的造价每米为a元,记锐角∠NBE=θ,总造价为W元. 
(1)试将W表示为θ的函数W(θ),并写出cosθ的取值范围;
(2)如何选取点M的位置,能使总造价W最小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com